2.2 Skalarprodukt (Fortsetzung)
Der Betrag \(|\overrightarrow{PQ}|\) eines Vektors \(\vec{x}=\overrightarrow{PQ}\) ist die Länge der Strecke \(PQ\). Für den Vektor \(\vec{p}=\left(\begin{array}{r}p_1\\p_2\\p_3\end{array}\right)\) erhält man die Länge \(|\vec{p}| = \sqrt{p_1^2+p_2^2 +p_3^2}\) indem man zweimal den Satz von Pythagoras anwendet.
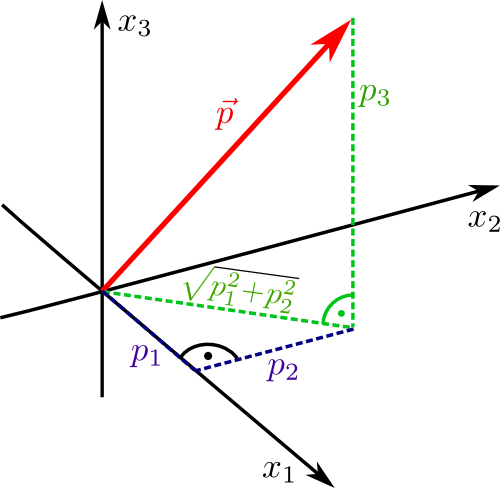
Der Betrag (die Norm) eines Vektors \(\vec{p}=\left(\begin{array}{r} p_1\\ p_2\\ p_3\end{array}\right)\) ist die reelle Zahl
\(|\vec{p}|=\sqrt{\langle\vec{p},\vec{p}\rangle}=\sqrt{p_1^2+p_2^2+p_3^2}.\)
Der Vorteil dieser Definition ist, dass sie sich ohne weiteres in beliebige Raumdimensionen übertragen lässt.
Für einen Vektor \(\vec{p}=\left(\begin{array}{r} p_1\\ \vdots \\ p_ n\end{array}\right)\in \mathbb {R}^n\) ist der Betrag bzw. die Norm definiert durch
\(|\vec{p}|=\sqrt{\langle\vec{p},\vec{p}\rangle}=\sqrt{p_1^2+p_2^2+\ldots+p_n^2}.\)
-
\(|\alpha \vec{x}|=|\alpha |\cdot |\vec{x}|\)
-
Insbesondere \(|-\vec{x}|=|\vec{x}|\)
-
\(|\overrightarrow {0}|=0\)
-
\(|\vec{x}+\vec{y}|\leq|\vec{x}|+|\vec{y}|\) (Dreiecksungleichung)
Mit Hilfe des Skalarprodukts lassen sich Winkel zwischen beliebigen Vektoren im \(\mathbb {R}^n\) festlegen.
\(\vec{x}\cdot\vec{y}=|\vec{x}|\cdot|\vec{y}|\cdot\cos\alpha\)
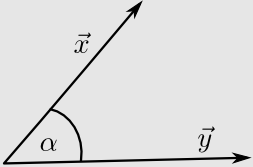
Insbesondere ist
\(\begin{align*} \vec{x}\cdot\vec{y}&> 0,\quad\textsf{ falls der Winkel ein spitzer Winkel ist}\\\vec{x}\cdot\vec{y}&= 0,\quad\textsf{ falls die Vektoren senkrecht aufeinander stehen}\\\vec{x}\cdot\vec{y}&< 0,\quad\textsf{ falls der Winkel ein stumpfer Winkel ist}\end{align*} \)
Als mathematische Randbemerkung sei erwähnt: Da \(\cos \alpha \) im Intervall \([-1,1]\) liegt, ergibt die Definition nur dann Sinn, wenn immer , d.h. für beliebige Wahl von \(\vec{x}\) und \(\vec{y}\)
\(\displaystyle\frac{\vec{x}\cdot\vec{y}}{|\vec{x}|\cdot|\vec{y}|}\in[-1,1]\)
ist. Dass dies tatsächlich immer so ist, ist die Aussage der Cauchy-Schwarz-Ungleichung.In der Mechanik begegnet man dem Skalarprodukt bei der Berechnung der physikalischen Arbeit. Wird eine Masse m durch eine Kraft \(\vec{F}\) in eine bestimmte Richtung \(\vec{s}\) verschoben, dann muss dazu die Arbeit (= Energie) \(\vec{F}\cdot \vec{s}\) aufgewendet werden. Da \(\vec{F}\) und \(\vec{s}\) nicht unbedingt dieselbe Richtung haben,zählt für die verrichtete
Arbeit nur derjenige Anteil der Kraft, der in die Richtung von \(\vec{s}\) zeigt.
