1.1 Mengen (Fortsetzung 4)
Eine weitere Regel gibt es für den Fall, dass man Durchschnitte und Vereinigungen von Mengen miteinander kombiniert.
Für drei beliebige Mengen A, B und C gilt:
\(\begin{aligned}(A\,\cap\,B)\,\cup\,C&= (A\,\cup\,C)\,\cap\,(B\,\cup\,C)\\ (A\,\cup\,B)\,\cap\,C &= (A\,\cap\,C)\,\cup\,(B\,\cap\,C)\end{aligned}\)
Auch diese Regeln kann man sich mit einer Zeichnung veranschaulichen:
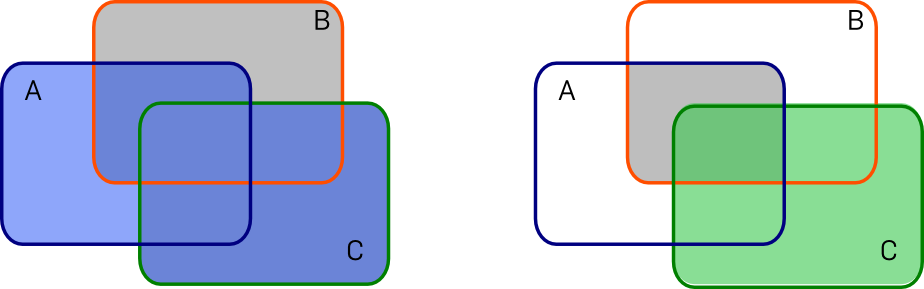
Auf der linken Seite sind \(A\,\cup\,C\) blau und \(B\,\cup\,C\) grau unterlegt. Den Durchschnitt dieser beiden Mengen erkennt man an der dunkleren Färbung. Auf der rechten Seite ist C grün und \(A\,\cap \,B\) grau unterlegt. Man erkennt nun, dass die Vereinigung der grün und grau unterlegten Mengen rechts genau mit dem dunkler gefärbten Gebiet links übereinstimmt.
Kartesisches Produkt von Mengen
Eine weitere Möglichkeit, aus schon bekannten Mengen neue Mengen zu konstruieren bietet das kartesische Produkt oder Kreuzprodukt:
Solche geordneten Paare kennen Sie vermutlich von Koordinaten in der Ebene. Dort gibt die erste Zahl die "x-Koordinate" und die zweite Zahl die "y-Koordinate" an.
Statt Paaren kann man auch n Objekte betrachten, die in einer bestimmten Reihenfolge zusammengefasst werden.
Geordnete n-Tupel spielen eine wichtige Rolle im Bereich der Datenstrukturen. Datenbanken enthalten oft n Einträge in einer festen Reihenfolge, die zusammengehören, wie (Artikelnummer,Name, Preis, Lieferzeit, Frachtkosten)
oder
(Name, Vorname, Matrikelnummer, Studienfach, Fachsemester)
Hier kann zum Beispiel der dritte Eintrag "‘Matrikelnummer"’ nur aus einer bestimmten Menge der vergebenen Matrikelnummern und der vierte Eintrag nur aus der Menge aller möglichen Studienfächer stammen.
Ein Computerprogramm kann nun problemlos die Namen aller Drittsemester im Fach Umweltingenieurwesen auslesen.
