24.4 Der Satz von Stokes
Der Satz von Stokes
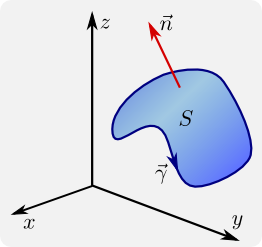
Der Satz von Stokes stellt eine Verbindung her zwischen einem Integral über eine Fläche S im $\mathbb{R}^3$ und einem Kurvenintegral entlang der geschlossenen Kurve, die die Fläche S begrenzt. Die Fläche muss dabei orientierbar sein. Das bedeutet anschaulich, dass sie eine "‘obere"’ und eine "‘untere"’ Seite besitzt. Man kann dann an jeder Stelle einen Normalenvektor definieren, so dass man diese Normalenvektoren auf der Fläche durch Verschieben ineinander überführen kann. Wenn die Fläche eine geschlossene Fläche ist, wie zum Beispiel eine Kugeloberfläche, dann kann man auswählen, ob die Normalenvektoren alle "‘nach außen"’ oder alle "‘nach innen"’ zeigen sollen.
Die allermeisten Flächen wie Kugeloberfläche, Zylinder oder Schaubilder von Funktionen, die von zwei Variablen abhängen, sind orientierbare Flächen, aber es gibt auch Flächen, die diese Eigenschaft nicht besitzen. Am bekanntesten darunter ist das Möbiusband, von dem im Foyer des NA-Gebäudes ein Modell ausgestellt ist.
$\displaystyle\int_{\vec{\gamma}}\vec{F}\,\mathrm{d}\vec{s}=\displaystyle\iint_{S}\mathrm{rot}\,\vec{F}\cdot \vec{n}\,\mathrm{d}\sigma$
Dabei wird die Richtung, in der $\vec{\gamma }$ durchlaufen wird, folgendermaßen festgelegt: Ein Beobachter, der in die Richtung des Normalenvektors $\vec{n}$ schaut, durchläuft $\vec{\gamma }$ so, dass S immer auf der linken Seite liegt. Wählt man also den "anderen" Normalenvektor, dann muss man entsprechend auch $\gamma$ in der entgegengesetzten Richtung durchlaufen.