23.3 Flussintegrale

Wir berechnen den Fluss des Vektorfeldes $\vec{F}(x,y,z) = (y,x,z^2)^ T$ durch die Mantelfläche des abgebildeten Zylinders (ohne Boden und Deckel) speziell für den Radius R = 3 und die Höhe h = 5.

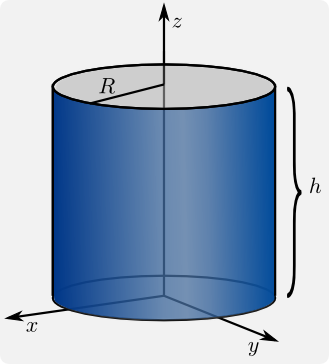
Die Parameterdarstellung der Mantelfläche in Zylinderkoordinaten ist>

$\vec{\Phi}(\varphi,z)=\left(\begin{array}{c}3\cos(\varphi)\\3\sin(\varphi)\\z\end{array}\right),\;\;\;\;\;0\leq z\leq 5,\;\;\;0\leq \varphi\leq 2\pi $

Das Vektorfeld in Zylinderkoordinaten ist $\vec{F}(x,y,z) = \left( \begin{array}{c}y\\ x\\ z^2\end{array} \right) = \left( \begin{array}{c}3\cdot \sin (\varphi )\\ 3 \cos (\varphi )\\ z^2\end{array} \right)$. Als nächstes berechnen wir den Normalenvektor.

$\begin{array}{rcl}\vec{\Phi}_{\varphi}\times\vec{\Phi}_z&=&\left(\begin{array}{c}-3\cdot \sin\varphi\\3\cdot \cos(\varphi)\\0\end{array}\right)\times\left(\begin{array}{c}0\\0\\1\end{array}\right)=\left(\begin{array}{c}3\cdot \cos\varphi\\3\cdot \sin(\varphi)\\0\end{array}\right)\end{array}$

Damit erhält man als Resultat für den Fluss durch die Mantelfläche

$\displaystyle\iint\limits_{Z}\vec{F}\cdot \vec{n}\,\mathrm{d}\sigma=\displaystyle\int\limits_{0}^{2\pi }\int\limits_0^{5}18\cos(\varphi)\sin(\varphi)\,\mathrm{d}z\,d\varphi=\displaystyle\int\limits_{0}^{2\pi }\int\limits_0^{5}9\sin(2\varphi)\,\mathrm{d}z\,d\varphi=0.$

Können Sie ein anschauliches Argument angeben, das bereits ohne Rechnung(!) zeigt, warum hier als Ergebnis am Ende 0 herauskommen muss?