22.1 Iterierte Integrale
Integration im $\mathbb{R}^2$
Die Grundaufgabe der eindimensionalen Integration in Kapitel 15 bestand darin, die Fläche zu berechnen, die zwischen der $x$-Achse und dem Schaubild $y=f(x)$ einer stetigen Funktion eingeschlossen ist. Wir betrachten nun eine analoge Aufgabe eine Raumdimension höher. Konkret betrachten wir eine nichtnegative stetige Funktion $f\colon [a,b]\times [c, d]\to [0,\infty )$. Es soll das Volumen $V$ des dreidimensionalen Körpers bestimmt werden, der zwischen dem Rechteck $R=[a, b]\times [c, d]$ und dem Schaubild $z=f(x,y)$ von $f$ liegt.
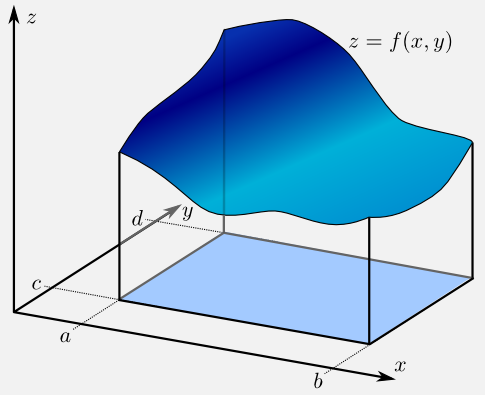
Wie im eindimensionalen Fall, bei dem das Intervall $[a,b]$ in immer kleinere Intervalle zerlegt wird, wählt man hier eine Partition $P$ des Rechtecks $R$ in $N$ kleinere Rechtecke $R_ k$ der Form $R_ k=[a_ k, b_ k]\times [c_ k, d_ k]$, die sich bis auf den Rand nicht überlappen und die das ganze Rechteck $R$ ausfüllen, also
$R=\bigcup\limits_{k=1}^NR_k.$
Ob man dazu ein Raster bildet oder das große Rechteck unregelmäßig in kleinere Rechtecke aufteilt, spielt für uns keine Rolle. In jedem Teilrechteck $R_ k$ seien $M_ k$ und $m_ k$ das Maximum beziehungsweise das Minimum der Funktion $f$ auf $R_ k$. Dann können wir das gesuchte Volumen nach unten und oben abschätzen durch
$\sum\limits_{k=1}^Nm_k\cdot |R_k|\leq V\leq\sum\limits_{k=1}^NM_k\cdot |R_k|$
wobei die Fläche des Rechtecks $R_ k$ wie gewohnt berechnet wird als $|R_ k| = (b_ k-a_ k)\cdot (d_ k-c_ k)$. Die linke Summe stellt also das Gesamtvolumen von Quadern mit der Grundfläche $R_ k$ und der Höhe $m_k$ dar, die rechte Summe entsprechend das Gesamtvolumen von Quadern mit der Grundfläche $R_ k$ und der Höhe $M_k$. Das gesuchte Volumen unter dem Graphen liegt immer zwischen diesen beiden Werten. Anschaulich liegen diese "Untersumme" und die "Obersumme" immer dichter beieinander, in je mehr kleine Rechtecke man das ursprüngliche Rechteck unterteilt. Insbesondere wird die Untersumme immer größer, wenn man die Rechtecke weiter unterteilt, während die Obersumme abnimmt.
Wie im eindimensionalen Fall muss man aber nicht unbedingt den kleinsten oder größten Wert betrachten, den die Funktion auf den Rechtecken annimmt, sondern kann auch den Funktionswert an irgendeiner Stelle des Rechtecks betrachten.
$Z_P(f)=\sum\limits_{k=1}^N(b_k-a_k)(d_k-c_k)f(\xi_j)$
Als Feinheit der Zerlegung definiert man den Flächeninhalt des größten in der Partition vorkommenden Rechtecks:
$\delta_P=\max\limits_k(b_k-a_k)(d_k-c_k)$
Eine beschränkte Funktion $f:[a,b]\times [c,d]\to \mathbb {R}$ heißt Riemann-integrierbar, wenn für jede Folge von Partitionen des Rechtecks $R$ mit Feinheit $\delta _ P\to 0$ die Folge der Riemann-Summen $Z_ P(f)$ konvergiert.
In diesem Fall definiert man das bestimmte (Riemann-)Integral von $f$ über das Rechteck $R$ als
$\displaystyle\iint\limits_Rf(x,y)\;\mathrm{d}x\;\mathrm{d}y=\lim\limits_{\delta_P\to 0}Z_P(f).$
