18.4 Taylorpolynome und Taylorreihen

Das Taylorpolynom von $\sin (x)$ zum Entwicklungspunkt $x_0=0$ erhält man, indem man beachtet, dass die Ableitungen der Sinusfunktion sich mit der Periode 4 wiederholen:

$\left(\sin(x)\right)'=\cos(x)$, $\;\left(\sin(x)\right)''=-\sin(x)$, $\;\left(\sin(x)\right)^{(3)}=-\cos(x)$, $\;\left(\sin(x)\right)^{(4)}=\sin(x)$ undsoweiter

Insbesondere haben daher die Ableitungen der Sinusfunktion an der Stelle \(x=0\) die Werte 0,1,0,-1,0,1,0,-1,0,.... Da die geraden Ableitungen verschwinden, treten im Taylorpolynom nur ungerade Potenzen auf. Dies liegt daran, dass die Sinusfunktion eine ungerade Funktion ist. Das Taylorpolynom der Sinusfunktion vom Grad 2n+1 lautet daher

\(T_{2n+1}(x;\sin,0)=x- \displaystyle\frac{x^3}{3!}+ \displaystyle\frac{x^5}{5!}-+\dots+(-1)^n \displaystyle\frac{x^{2n+1}}{(2n+1)!}\)

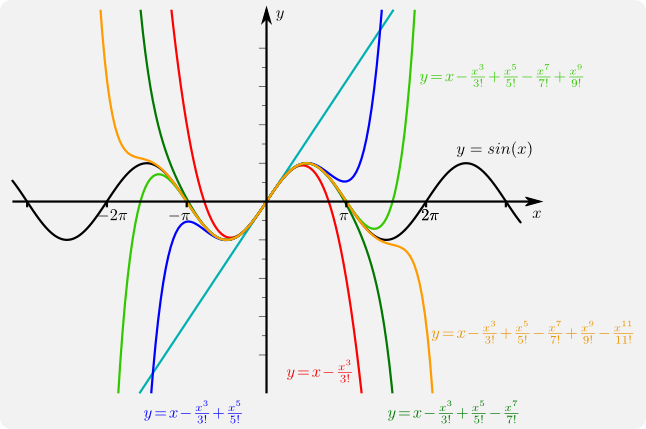
Analog kann man Taylorpolynome der Cosinusfunktion zum Entwicklungspunkt \(x_0=0\) bestimmen und stellt fest, dass nur gerade Potenzen vorkommen. Genauer ergibt sich

$T_{2n}(x;\cos,0)=1-\displaystyle\frac{x^2}{2!}+\displaystyle\frac{x^4}{4!}-+\dots+(-1)^n\displaystyle\frac{x^{2n}}{(2n)!}$

Cosinus und Sinus haben für alle $x\in \mathbb {R}$ die Potenzreihendarstellung

$\begin{array}{rcl}\sin(x)&=&\displaystyle\sum\limits_{n=0}^{\infty}\displaystyle\frac{(-1)^n}{(2n+1)!}x^{2n+1}\\\cos(x)&=&\displaystyle\sum\limits_{n=0}^{\infty}\displaystyle\frac{(-1)^n}{(2n)!}x^{2n}.\end{array}$

Diese "Reihenentwicklungen" haben eine große praktische Bedeutung, denn

• zum einen kann man für praktische Rechnungen und solange |x| einigermaßen klein ist, nichtlineare Terme wie $\sin (x)$ durch den oder die ersten Terme der Reihe ersetzen und

• zum anderen kann man das Grenzwertverhalten von Funktionen manchmal leicht verstehen, wenn man die Potenzreihen verwendet. Beispielsweise ist

  $\lim\limits_{x\to 0}\displaystyle\frac{x\sin(x)}{\cos(x)-1}=\lim\limits_{x\to 0}\displaystyle\frac{x(x-\frac{x^3}{3!}+\frac{x^5}{5!}-+\dots)}{1-\frac{x^2}{2!}+\frac{x^4}{4!}-+\dots-1}=\lim\limits_{x\to 0}\displaystyle\frac{x^2+\dots}{-\frac{x^2}{2!}+\dots}=-2$