18.2 Konvergenzkriterien
Das Majorantenkriterium
Eine Variante des Sandwich-Kriteriums für Reihen ist das Majorantenkriterium. Allerdings ist der Beweis etwas komplizierter und kann nicht allein mit Hilfe des Sandwich-Kriteriums geführt werden. Auch hier wäre das oben angesprochene Cauchy-Kriterium das richtige Werkzeug.
Sei $\sum \limits _{k=1}^{\infty } a_ k$ eine beliebige Reihe mit $|a_ k|\leq b_k$ für alle k und $\sum \limits _{k=1}^{\infty } b_ k$ eine konvergente Reihe.
Dann konvergiert auch die Reihe $\sum\limits _{k=1}^{\infty } a_k$ und die Reihe $\sum \limits _{k=1}^{\infty } b_ k$ heißt Majorante zur Reihe $\sum \limits _{k=1}^{\infty } a_k$.
Anschaulich entspricht die Summe $\sum b_k$ genau dem Flächeninhalt von Rechtecken mit der Höhe $b_k$ und der Breite $1$. Ist der gesamte Flächeninhalt $\sum b_k$ der größeren Rechtecke endlich, dann ist auch der Flächeninhalt $\sum |a_k|$ der kleineren Rechtecke endlich.
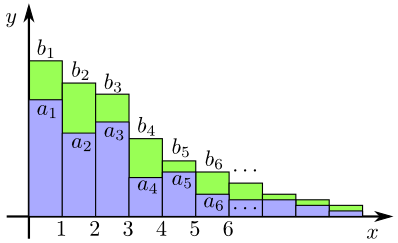
Etwas präziser kann man das mit Hilfe des Satz über positive Reihen formulieren: Die Partialsummen $S_n=\sum\limits_{k=1}^n |a_k|$ bilden eine monoton wachsende Folge $(S_n)_{n\in\mathbb{N}}$, die aber wegen
\( S_n = \displaystyle\sum\limits_{k=1}^n |a_k| \leq \displaystyle\sum\limits_{k=1}^n b_k \leq \displaystyle\sum\limits_{k=1}^\infty b_k \)
von oben beschr\"ankt ist und daher konvergent sein muss. Diese Konvergenz bedeutet aber gerade, dass die Reihe $\sum\limits_{k=1}^{\infty} a_k$ (absolut) konvergiert.
$\dfrac{1}{k^2}\leq\dfrac{1}{k(k-1)}$
denn der Bruch wird größer, wenn der Nenner kleiner wird. Für die Partialsummen der Reihe $\sum \limits _{k=2}^{\infty }\dfrac {1}{k(k-1)}$ gilt aber$\sum\limits_{k=2}^N\dfrac{1}{k(k-1)}=\sum\limits_{k=2}^N\left(\dfrac{1}{k-1}-\dfrac{1}{k}\right)=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+-\dots+\dfrac{1}{N-1}-\dfrac{1}{N}=1-\dfrac{1}{N}$
Damit konvergieren die Partialsummen für $N\to \infty $ gegen 1 und die Reihe $\sum \limits _{k=2}^{\infty }\dfrac {1}{k(k-1)}$ ist eine konvergente Majorante für die Reihe $\sum \limits _{k=2}^{\infty }\dfrac {1}{k^2}$, die daher auch konvergieren muss. Der Wert dieser Reihe ist auch bekannt: Er beträgt genau $\dfrac{\pi^2}{6}$, aber das ist mit unseren aktuellen mathematischen Fähigkeiten nur sehr schwer zu zeigen.