19.3 Gradient und Richtungsableitung
Der Gradient einer Funktion
Die partiellen Ableitungen einer Funktion fasst man oft in einem Vektor zusammen.
Sei \(U\subset \mathbb {R}^ n\) und $f:U\to \mathbb{R}$ eine Funktion, deren partielle Ableitungen im Punkt \(\vec{a}\) alle existieren. Dann heißt der Vektor
\(\mathrm{grad}f(\vec{a})=\left(\begin{array}{c}\frac{\partial f}{\partial x_1}(\vec{a})\\\vdots\\\frac{\partial f}{\partial x_n}(\vec{a})\end{array}\right)\)
Gradient von \(f\) im Punkt \(\vec{a}\). Eine andere Schreibweise dafür ist \(\vec{\nabla } f(\vec{a})\) (Das auf den Kopf gestellte Dreieck heißt "Nabla").
Der Gradient einer Funktion wird meistens als Spaltenvektor, manchmal aber auch als Zeilenvektor aufgefasst. Man sollte sich darüber im Klaren sein, dass beide Möglichkeiten vorkommen können. Die Schreibweise als Zeilenvektor hat den Vorteil, dass sie zu den später definierten Jacobi-Matrizen für die Ableitung von Funktionen \(f:\mathbb {R}^ m\to \mathbb {R}^ n\) passen.
Sei \(U\subset \mathbb {R}^n\) und \(f:U\to \mathbb {R}\) eine Funktion, die nach allen Variablen partiell differenzierbar ist. Dann zeigt der Gradient \(\mathrm{grad} f(\vec{a})\) in die Richtung des stärksten Anstiegs von \(f\) im Punkt \(\vec{a}\). Entsprechend zeigt \(-\mathrm{grad} f(\vec{a})\) in die Richtung des stärksten Gefälles
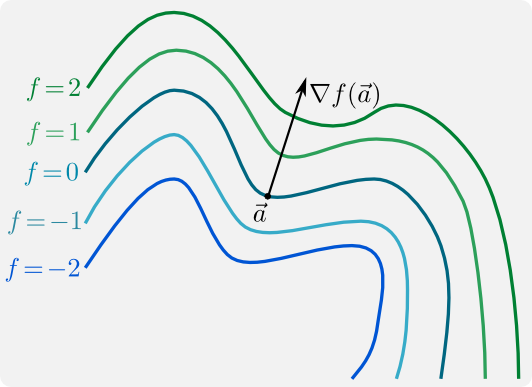
Der Gradient \(\mathrm{grad}\, f(\vec{a})\) steht außerdem senkrecht auf den Niveaumengen von \(f\), d.h. auf denjenigen Kurven oder Flächen, auf denen \(f\) einen konstanten Wert hat.
