19.3 Gradient und Richtungsableitung

Die Tangentialebene an ein Funktionsschaubild ist diejenige Ebene, die sich dem Schaubild einer Funktion von zwei Variablen in der Nähe eines Punktes am besten anpasst.

Hat man eine Funktion einer Veränderlichen, z.B. \(y=f(x)=e^ x-3x^2+2\), so kann man an jeden Punkt \((x_0,f(x_0))\) auf der Kurve eindeutig eine Tangente anlegen. Diese wird durch die Gleichung \(y=f(x_0)+f’(x_0)(x-x_0)\) beschrieben.

Bei einer Funktion von zwei Variablen gibt es durch jeden Punkt des Schaubilds unendlich viele Geraden, deren Steigung jeweils der Richtungsableitung der Funktion an dieser Stelle entsprechen. Diese Geraden spannen gemeinsam die Tangentialebene an diesem Punkt auf.

Wenn man sich an die Parameterdarstellung von Ebenen aus MatheMaterialien 1 erinnert, dann benötigt man den Ortsvektor eines Punktes, der in der Ebene liegt, sowie zwei Richtungsvektoren, um eine Ebene festzulegen.

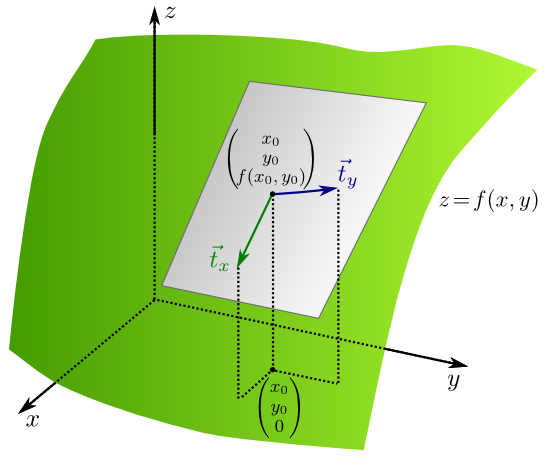
Als Punkt wählt man natürlich den Punkt \((x_0,y_0,f(x_0,y_0))\) auf dem Schaubild. Die beiden Richtungsvektoren erhält man, indem man das Schaubild jeweils mit einer Ebene \(\{ (x,y,z);\,y=y_0\} \) bzw. \(\{ (x,y,z);\,x=x_0\} \) parallel zu den Koordinatenebenen schneidet. Tangentialvektoren an das Schaubild, die in diesen Ebenen liegen sind dann

\( \vec{t}_x=\left(\begin{array}{c}1\\0\\\frac{\partial f}{\partial x}(x_0,y_0)\end{array}\right),\quad\vec{t}_y=\left(\begin{array}{c}0\\1\\\frac{\partial f}{\partial y}(x_0,y_0)\end{array}\right)\)

Die Tangentialebene im Punkt \((x_0,y_0,f(x_0,y_0))\) hat dann die Darstellung

\( \vec{x}=\left(\begin{array}{c}x_0\\y_0\\f(x_0,y_0)\end{array}\right)+s\cdot \left(\begin{array}{c}1\\0\\\frac{\partial f}{\partial x}(x_0,y_0)\end{array}\right)\,+t\cdot \left(\begin{array}{c}0\\1\\\frac{\partial f}{\partial y}(x_0,y_0)\end{array}\right).\)

Möchte man die Ebene in Hesse-Normalform angeben, benötigt man dazu den Normalenvektor \(\vec{n}\), der auf den beiden angegebenen Tangentialvektoren senkrecht steht. Den (auf die Länge 1 normierten) Normalenvektor erhält man mit Hilfe des Kreuzprodukts:

\( \vec{n}=\displaystyle\frac{\vec{t}_x\times\vec{t}_y}{\left|\vec{t}_x\times\vec{t}_y\right|}=\displaystyle\frac{1}{\sqrt{1+\frac{\partial f}{\partial x}(x_0,y_0)^2+\frac{\partial f}{\partial y}(x_0,y_0)^2}}\left(\begin{array}{c}-\frac{\partial f}{\partial x}(x_0,y_0)\\-\frac{\partial f}{\partial y}(x_0,y_0)\\1\end{array}\right) \)

Die Hessesche Normalform lautet dann

\( \displaystyle(\vec{x},\vec{n})=d\,\,\text{mit}\,\,\,d=\left(\begin{array}{c}x_0\\y_0\\f(x_0,y_0)\end{array}\right)\cdot \vec{n}. \)