19.1. Funktionen im R^n
Konvergenz und Stetigkeit im $\mathbb{R}^n$
Wenn wir im mehrdimensionalen Raum differenzieren und später auch integrieren wollen, müssen wir Grenzwerte bilden können. Wir müssen also zum Beispiel wissen, was es heißt, wenn eine Folge von Punkten im \(\mathbb {R}^n\) konvergiert. Eine Folge \(\vec{x}_1,\vec{x}_2,\vec{x}_3,\ldots\) im \(\mathbb{R}^n\) besteht aus lauter Punkten, von denen jeder im $\mathbb {R}^ n$ liegt. Um diese Punkte mit ihren Komponenten aufzuschreiben, benötigen wir einen zweiten Index, also zum Beispiel
\(\vec{x}_k=(x_k^{(1)},\dots,x_k^{(n)}).\)
Der untere Index ist hier der Folgenindex, der obere gibt die Komponente des Vektors an.
Die Definition von Konvergenz können wir aus dem Eindimensionalen auf Folgen von Vektoren übertragen, da es dabei nur um den Abstand der Folgenglieder zum Grenzwert geht.
Eine Folge \((\vec{x}_k)_{k\in \mathbb {N}}\) von Punkten \(\vec{x}_k\in \mathbb {R}^n\) konvergiert gegen den Grenzwert \(\vec{a}\in \mathbb{R}^n\), falls
\(\lim\limits_{k\to \infty}|\vec{x}_k-\vec{a}|=0.\)
Die Schreibweise ist wie bei reellen Folgen \(\vec{a} = \lim \limits_{k\to \infty } \vec{x}_k\).
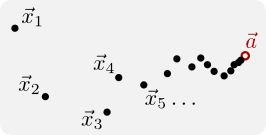
Man beachte, dass \((|\vec{x}_k -\vec{a} |)_{k\in \mathbb {N}}\) eine Folge reeller Zahlen ist, denn der Abstand von zwei Vektoren ist eine (nicht-negative) Zahl. Die Konvergenz von solchen Folgen kennen wir aber schon aus Kapitel 10.
Anschaulich bedeutet die Konvergenz der Folge \((\vec{x}_k)_{k\in \mathbb {N}}\) gegen \(\vec{a}\), dass in jeder noch so kleinen Kugel um den Punkt \(\vec{a}\) alle Folgenlieder ab einem bestimmten Index $K$ liegen. Etwas formaler: Wenn man eine beliebige Zahl $\varepsilon > 0$ vorgibt, dann kann man dazu einen Anfangsindex \(K=K(\varepsilon )\) finden, so dass für $k=K+1, K+2,K+3,\ldots$ immer \(|\vec{x}_k -\vec{a} |<\varepsilon\) ist.
$\lim\limits_{k\to \infty}x_{k}^{(j)}=a_j.$
Begründung: Zum Beweis benutzen wir gleich zweimal das Sandwichkriterium für Zahlenfolgen.
Für einen beliebigen Index $j\in \{ 1,2,\dots ,n\} $ gilt die Abschätzung
$0\leq |x_k^{(j)}-a_j|=\sqrt{(x_k^{(j)}-a_j)^2}=\sqrt{(x_k^{(1)}-a_1)^2+(x_k^{(2)}-a_2)^2+\ldots +(x_k^{(n)}-a_n)^2}=|x-a|$
d.h. falls $|\vec{x}_k-\vec{a}|$ für $k\to \infty $ gegen $0$ strebt, dann konvergiert auch $|x_k^{(j)}-a_j|\to 0$ nach dem Sandwich-Kriterium. Das bedeutet aber gerade, dass die $j$-te Kompontente $x_k^{(j)}$ für $k\to \infty$ gegen $a_j$ konvergiert.
Andererseits ist
$ \begin{array}{rcl}&&\left(|x_k^{(1)}-a_1|+\ldots +|x_k^{(1)}-a_n|\right)^2\\ &=&\underbrace{|x_k^{(1)}-a_1|^2+\ldots +|x_k^{(n)}-a_n|^2}_{\text{rein quadratische Terme}}+\underbrace{2\sum\limits_{i\neq j}|x_k^{(i)}-a_i|\cdot |x_k^{(j)}-a_j|}_{\text{gemischte Glieder}}\\&\geq &\left(x_k^{(1)}-a_1\right)^2+\left(x_k^{(2)}-a_2\right)^2+\ldots +\left(x_k^{(n)}-a_n\right)^2\end{array}$
indem man die gemischten Glieder einfach weglässt, und damit
$\begin{array}{rcl} 0\leq |\vec{x}_k-\vec{a}| & = & \sqrt{(x_k^{(1)}-a_1)^2+(x_k^{(2)}-a_2)^2+\ldots +(x_k^{(n)}-a_n)^2} \\ & \leq & |x_k^{(1)}-a_1|+\ldots +|x_k^{(1)}-a_n|.\end{array}$
Wenn also alle Ausdrücke \(|x_k^{(j)}-a_j|\) auf der rechten Seite für $k\to \infty $ gegen Null konvergieren, dann konvergiert auch $|\vec{x}_k-\vec{a}|\to 0$.
❑
Wenn man Grenzwerte im $\mathbb{R}^ n$ kennt, dann kann man sofort die Definition der Stetigkeit auch auf Funktionen von $n$ Variablen übertragen.
Sei \(U\subset \mathbb {R}^n\). Eine Funktion $f\colon U\to \mathbb {R}$ heißt stetig im Punkt $\vec{a}$, wenn für jede Folge $\vec{x}_1,\vec{x}_2,\ldots$, die gegen $\vec{a}$ konvergiert gilt:
$\lim\limits_{k\to \infty}f(\vec{x}_k)=f(\vec{a}).$
Man schreibt auch \(\lim\limits_{\vec{x}\to \vec{a}}f(\vec{x})=f(\vec{a})\).
f heißt stetig auf \(U\), wenn f in allen Punkten \(\vec{a}\in U\) stetig ist.
- Anschaulich bedeutet Stetigkeit wieder, dass der Graph einer stetigen Funktion keine "Sprünge" oder "Stufen" hat.
- Bei der Untersuchung einer Funktion auf Stetigkeit geht es zunächst wieder um dieselben Themen wie im Eindimensionalen (Wird ein Nenner Null? Kann ein Term unter der Wurzel negativ werden? etc.)
- Eine vektorwertige Funktion \(\vec{f}:\mathbb {R}^n\to \mathbb {R}^m\) ist stetig im Punkt \(\vec{a}\), wenn alle Komponenten von \(\vec{f}\) in \(\vec{a}\) stetig sind.
Im ersten Teil der MatheMaterialien hatten wir gesehen, dass Funktionen, die auf einem abgeschlossenen Intervall \([a,b]\) stetig sind, dort sehr vorteilhafte Eigenschaften besitzen. Beispielsweise sind sie beschränkt, das heißt, die Funktionswerte lagen in einem endlichen Intervall.
Außerdem nimmt eine auf \([a,b]\) stetige Funktion ihr Maximum und ihr Minimum in (mindestens) einem Punkt an. Für die Nullstellensuche ausgesprochen nützlich war darüberhinaus der Zwischenwertsatz, der ebenfalls auf der Stetigkeit beruhte.
Erinnerst Du Dich noch, was der Zwischenwertsatz aussagt?
► Klicken, um die Antwort anzuzeigen.
Der Zwischenwertsatz sagt aus, dass eine auf \( [a,b] \) stetige Funktion \(f\) jeden Wert zwischen \( f(a) \) und \(f(b)\) (mindestens) einmal annimmt.
