Kursinformation

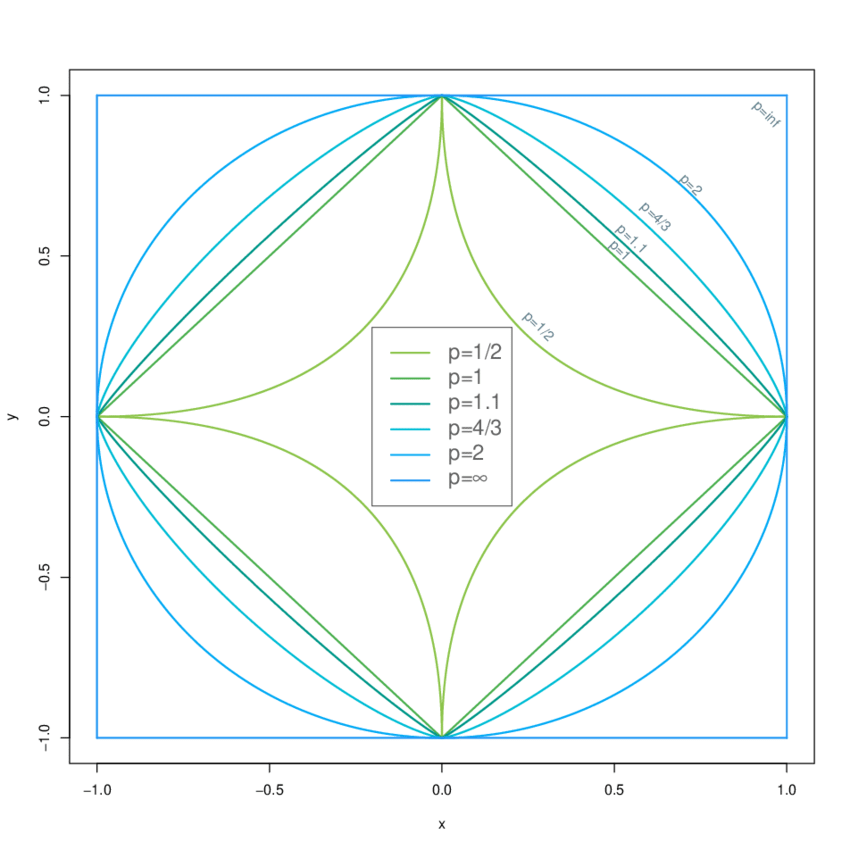
In dieser Vorlesung behandeln wir ausgewählte Themen aus der aktuellen Forschung an der Schnittstelle zwischen Geometrie und Stochastik. Im ersten Teil beschäftigen wir uns mit hochdimensionalen konvexen Körpern und zeigen, dass diese ähnlichen Gesetzmäßigkeiten unterliegen, wie Summen von unabhängigen Zufallsvariablen. Insbesondere beweisen wir zentrale Grenzwertsätze und Prinzipien großer Abweichungen für hochdimensionale $\ell_p$-Kugeln und diskutieren verschiedene geometrische Anwendungen. Im Zentrum des zweiten Teils der Vorlesung steht die Theorie der konischen inneren Volumina. Wir führen den Begriff der statistischen Dimension ein und entwickeln Konzentrationsungleichungen, die eine wichtige Rolle in der Optimierung spielen. Darüber hinaus beschäftigen wir uns mit zufälligen Projektionen regulärer Polytope in hohen Dimensionen. In einem möglichen dritten Vorlesungsteil beweisen wir den berühmten Satz von Gluskin über den Durchmesser des Banach-Mazur-Kompaktums und verbinden dies mit einer Einführung in die spannende Theorie der zufälligen Polytope.