Das Wasserstoffatom

Aufspaltung des Spektrum bis ins kleinste Detail

Letzte Vorlesung

Lösung der Schrödinger-Gleichung für das Wasserstoffatom

  • Annahmen:

    1. Das Wasserstoffsystem lässt sich beschrieben über ein statisches Proton im Zentrum und ein dynamisches nicht-relativistisches Elektron, weleche über die Coulombwechselwirkung miteinander interagieren

      $$ V_C = -\frac{1}{4 \pi \epsilon_0} \frac{e^2}{r}$$

      $\Rightarrow$ Das System kann über die Schrödinger-GL beschrieben werden

    2. Das Elektron ist gebunden ($E < 0$)

    Hinweis: Man macht keine Annahme über quantisierte Bahnen!

  • Lösungen:

    • $ \psi_{n l m}(r, \vartheta, \varphi) =c_{n l}\left(\frac{2 r}{a_{0} n}\right)^{l} \exp \left\{-\frac{r}{a_{0} n}\right\} L_{n+l}^{2 l+1}\left(\frac{2 r}{a_{0} n}\right) Y_{l m}(\vartheta, \varphi) $

    • $E_{n}=-\frac{m e^{4}}{8 \epsilon_{0}^{2} h^{2}} \frac{1}{n^{2}}$ (wird nur durch $n$ bestimmt)

Orbitale

wikipedia.org: atomic orbital

Orbitale besitzen Maximum $r_{nlm}^\mathrm{max} = \mathrm{max}_r(r^2 |\psi_{nlm}|^2)$ wie von Bohr postuliert: $r_n = r_0 n^2$

Allerdings extistieren auch Maxima an Punkten mit $r \neq n^2 r_0$!

Feinstruktur: Idee (Zeeman-Effekt)

  • (Klassisch:) Bewegte Ladungen erzeugen ein magnetisches Moment

    $$ \boldsymbol{\mu}=\frac{1}{2} \int \mathrm{d}^{3} \boldsymbol{r}[\boldsymbol{r} \times \boldsymbol{j}(\boldsymbol{r})] $$

  • Mit dem QM Wahrscheinlichkeitsstrom des Elektrons ergibt sich, dass dieses Moment proportional zu der $m$ Quantenzahl ist $$\mu_z=-\frac{e}{2 m_{\mathrm{e}}}m_l \equiv - \mu_B m_l$$

  • Über die Equivalenz lässt sich somit der magnetische Moment Operator über den Drehimpuls einführen

    $$ \hat{\mu}_z \equiv - \frac{\mu_B}{\hbar}\hat{L}_z$$

  • Da Oribitale für unterschiedliche $m_l$ unterschiedliche Elektronenbewegungen zulassen, muss somit folglich, für ein externes magnischtisches Feld, die Energie $m_l$ abhängig sein

    $ \hat H \to \hat H + \hat \mu_z B_z^{\mathrm{ext}}$ und

    $E_n \to E_{n m_l} = E_n - \mu_B B_z^{\mathrm{ext}} m_l + \cdots$

Erwartung:

Aufspaltung der Energieniveaus durch externes Magnetfeld

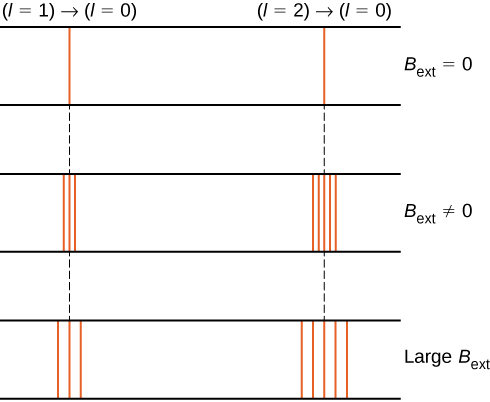
Erwartete Übgergänge erzeugen ein Linienspektrum mit verschobenen Wellenlängen

University Physics 3

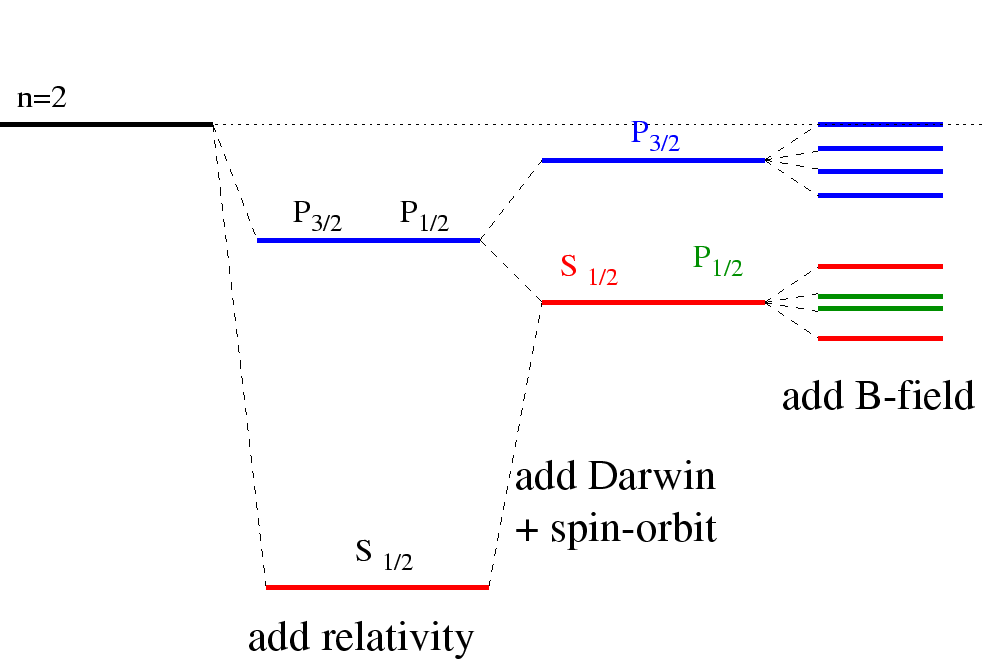
Feinstruktur

Beobachtungen

  1. Ein externes Magnetfeld spaltet die Linien, aber man findet weniger/andere Linien als erwartet und auch $l=0$ (S-Orbital) Zustände spalten sich
  2. Energieniveaus sind kleiner als erwartet

Folgerungen

  1. Es muss andere Drehungszustände geben als erwartet: halbzahlige Drehungen müssen erlaubt sein.
  2. Es gibt weitere Korrekturen die, mir dieser Genauigkeit, eine Rolle spielen

Lösungsansätze

  1. Auch das Elektron besitzt eine Eigendrehung, genannt Spin $s$, die mit dem Drehimpuls zu einer Gesammtdrehung koppelt $j$.

    $\hat{\boldsymbol{J}} = \hat{\boldsymbol{L}} + \hat{\boldsymbol{S}}$

    Dieser spin ist halbzahlig mit

    $\hat S_z |s, m_s \rangle = \hbar m_s |s, m_s \rangle$ und $m_s = \pm \frac{1}{2}$

  2. Relativistische Korrekturen spielen eine Rolle

Feinstruktur: Formalismus

Welche Größen spielen wann eine Rolle?

  • Da es den $\hat \mu_J = \hat \mu_L + \hat \mu_S = \mu_B \hat L + \mu_e \hat S$ Opertor gibt, muss es auch den folgenden Term geben:
    (Effektive Theorien: Was nicht explizit ausgeschlossen ist, das ist erlaubt)

    $\hat H = \hat H_0 + \lambda \hat{ \boldsymbol S} \cdot \hat{ \boldsymbol L}$ ... die sogenannte Spin-Orbit Koppelung

quantummechanics.ucsd.edu

  • Welche weiteren Größen gibt es und welche sind relevant?

    Die Energie lässt sich über zwei fundamentale Parameter beschreiben:

    $\displaystyle -E_{n, B o h r}=\frac{m_e e^{4}}{2\left(4 \pi \epsilon_{0} \hbar\right)^{2}} \frac{1}{n^{2}}$ $=\frac{1}{2}\left(\frac{e^{2}}{4 \pi \epsilon_{0} \hbar c}\right)^{2} m_e c^{2} \frac{1}{n^{2}}$ $=\alpha^{2} \frac{m_e c^{2}}{2} \frac{1}{n^{2}}$

    Mit der Stärke der EM Wechselwirkung $\alpha \equiv\frac{e^{2}}{4 \pi \epsilon_{0} \hbar c} \simeq \frac{1}{137}$ und der Ruheenergie des Elektrons $m_e c^2$

  • Die Korrektur zum (relativistischen) Hamiltonian der die Feinstruktur beschreibt ist somit (ohne externes Magnetfeld)

    $\displaystyle \frac{\hat{H}}{m_e c^{2}}= \overbrace{\underbrace{\frac{\hat{\boldsymbol{p}}^{2}}{2 m_e^2c^2} + \frac{V(\hat r)}{m_e c^{2}}}_{\text{Ursprungshamiltonian}}}^{\mathcal O(\alpha^2) } $ $\displaystyle + \underbrace{ 1 -\overbrace{\frac{\hat{\boldsymbol{p}}^{4}}{8 m_e^{4} c^{4}} -\frac{\hbar^{2}\Delta V(\hat r)}{8 m_e^{4} c^{4}}}^{ \mathcal O(\alpha^4) } }_{\text{rel. Korrekturen}} $ $\displaystyle + \underbrace{\overbrace{\lambda \hat{L} \cdot \hat{S}}^{\mathcal O(\alpha^4) } }_{\text { Spin-Orbit-Kopplung }}$
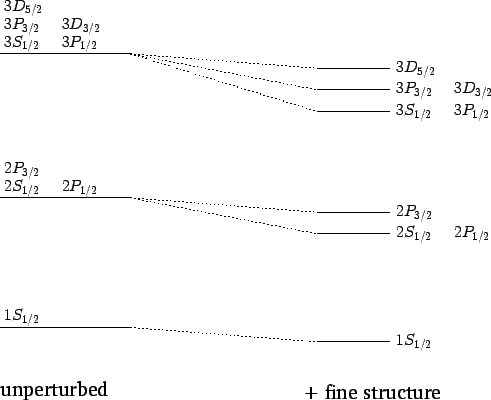
    und mit $ E_{nj} =-\frac{13,6 \mathrm{eV}}{n^{2}}\left[1+\frac{\alpha^{2}}{n^{2}}\left(\frac{n}{j+\frac{1}{2}}-\frac{3}{4}\right)\right] $

Noch bessere Auflösung

  • Quantisierung der Coulombwechselwirkung (Quantum Elektrodynamik): Lamb-Shift $\sim \alpha^5$(Selbstenergie des Elektrons, Vakuumspolarisation und anomales magnetisches Moment (Vertexkorrektur))

  • Berücksichtigung des Protons (und des Proton Spin): Hyperfeinstruktur $\boldsymbol\mu_p \cdot \boldsymbol\mu_e\sim \alpha^4 m_e / m_p$

wikimedia.org

  • Die Radio-Welle assoziert mit dem Proton-Spin mit $\lambda = 21$cm ($\approx 42/2$cm) spielt eine große Rolle: Radio astronomy & Big Bang, Kernspinresonanz & Magnetresonanztomographie, Quantum Computing mit Ionenfalle