Aus der Vorlesung
Der Drehimpulsoperator
-
Der Drehimpulsoperator ist definiert über das Kreuzprodukt von Ort- und Impulsoperator
$\hat{L}_{i} \equiv (\hat{\vec x} \times \hat{\vec p})_i \equiv \sum\limits_{j,k=1}^3 \epsilon_{i j k} \hat x_j \hat p_k $
-
Er erfüllt die Kommutationsrelation ($SO(3)$-Gruppe aber $su(2)$-Algebra)
$\left[\hat{L}_{i}, \hat{L}_{j}\right]=i \hbar \sum\limits_{k=1}^3 \epsilon_{i j k} \hat{L}_{k}$ und $\left[\hat{\vec{L}}^{2}, \hat{L}_{i}\right]=0$
-
Eigenzustände dieses Operators können über Drehimpulszahlen $l, m$ definiert werden
$\hat{L}^{2}|\psi_{lm}\rangle=\hbar^{2} l(l+1)|\psi_{lm}\rangle $ mit $l \in \mathbb{N}_0$ und $ \hat{L}_{3}|\psi_{lm}\rangle=m \hbar|\psi_{lm}\rangle $ und $m \in \mathbb{Z}$ aber $-l \leq m \leq l$
Technisch gesehen erlaubt die Algebra auch halbzahlige Spins (Fermionen; später), aber der Drehimpuls selbst existiert nur für ganzzahlige $l,m$
-
Für konservative Kraftsysteme im Ortstraum (sphärische Koordinaten) wird sich die Schrödinger-Gleichung somit zu
$\displaystyle\small\hat{H}=\frac{\hat{\vec{p}}^{2}}{2 m}+V(\hat r)=\frac{\hat{p}_{r}^{2}}{2 m}+\frac{\hat{L}^{2}}{2 m r^{2}}+V(\hat r)$
mit $\small\hat{p}_{r}^{2}=-\hbar^{2} \frac{1}{r^{2}} \frac{\partial}{\partial r}\left[r^{2} \frac{\partial}{\partial r}\right]$ und $\small\hat{L}^{2}=-\hbar^{2}\left\{\frac{1}{\sin \vartheta} \frac{\partial}{\partial \vartheta}\left(\sin \vartheta \frac{\partial}{\partial \vartheta}\right)+\frac{1}{\sin ^{2} \vartheta} \frac{\partial^{2}}{\partial \varphi^{2}}\right\}$
-
Eigenfunktionen des Drehimpulsoperators im Ortsraum sind die Kugelfächenfunktionen $Y_{lm}(\theta, \phi)$
$\langle \vec r |\psi_{lm}\rangle = \psi(r) Y_{lm}(\theta, \phi)$
Aus der Vorlesung
Das Wasserstoffatom
Als spezielles Beispiel für konservative Kraftsysteme in der Quantenmechanik
-
Als gute Näherung kann das Wasserstoffatom als statisches Proton im Ursprung welches elektrisch mit einem nicht-relativistischen Elektron wechselwirkt beschrieben werden
$V(\hat{\vec r}) = V(\hat r)=-\frac{e^{2}}{4 \pi \epsilon_{0} \hat r}$ und $m = m_e$
-
Die Lösung der SGL $\langle \vec r |\psi_{nlm}\rangle = R_{nl}(r) Y_{lm}(\theta, \phi)$ wird beschrieben durch
-
Den Winkelanteil mit Kugelfächenfunktionen $ Y_{lm}(\theta, \phi)$
-
Den radialen Anteil $ R_{nl}(r)$ für gebundene Zustände $E<0$ mit
$$ \small R_{n l}(r)=\frac{u_{l}(r)}{r} = c_{n l}\left(\frac{2 r}{a_{0} n}\right)^{l} \exp \left\{-\frac{r}{a_{0} n}\right\} L_{n+l}^{2 l+1}\left(\frac{2 r}{a_{0} n}\right)$$
- $L_{j}^{k}(x)$ sind assoziierte/zugeordnete Laguerre-Polynome
- $ \small c_{n l} = \sqrt{\left(\frac{2}{n a_{0}}\right)^{3} \frac{(n-l-1) !}{2 n[(n+l) !]^{3}}}$ die Normierungskonstante
- $a_0 = \frac{4 \pi \epsilon_{0} \hbar^{2}}{e^{2} m}$ der Bohrsche Radius
-
-
Die $n$-Quantenzahl (Haupt- oder Energiequantenzahl) mit $n \in \mathbb N_0$ begrenzt die Drehimpulszahl $0 \leq l \leq n-1$ und sorgt für die bereits bekannte Quantisierung des Linienspektrums $\small E_{n}=-\frac{m e^{4}}{8 \epsilon_{0}^{2} h^{2}} \frac{1}{n^{2}} $
- Siehe auch das Widget (falstad.com) für Darstellungen der Wellenfunktion
Hausaufgabe Blatt 7
3D Darstellung von Kugelfächenfunktionen
Die Kugelflächenfunktionen $Y_{lm}(\theta,\phi)$ sind im Allgemeinen komplexwertig. Eine Möglichkeit sie dreidimensional darzustellen, ist es, ihren Realteil, Imaginärteil oder Betrag abhängig von den Raumwinkeln $\theta$ und $\phi$ als Abstand vom Ursprung zu geben.
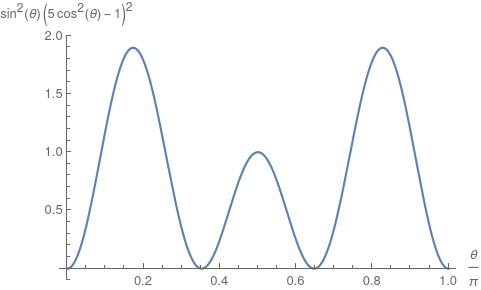
Beispiel: Wir wollen den Plot folgender Funktion betrachten: $$(\text{Re}(Y_{31}))^2 =\frac{21}{64 \pi}\cos^2(\phi)(5\cos^2(\theta)-1)^2\sin^2(\theta)$$
Die Graphen des $\phi$- und $\theta$ Teil ergeben sich zu:

Sodass der 3D Plot des Realteils von $Y_{31}$ zum Quadrat gegeben ist wie folgt (wobei der positive Realteil rot und der negative Realteil grün eingefärbt sind):
