Aus der Vorlesung

Der 1D harmonische Oszillator

  • Der harmonische Oszillator beschreibt System nahe eines Minimums des potentials und ist somit eine gute Approximation für viele physikalische Systeme.

  • Lösungen des 1D harmonischen Oszillators lassens sich über Hermiteschen Polynome beschreiben

    $ \psi_{n}(z, t)=\left(\frac{m \omega}{\pi \hbar}\right)^{1 / 4} \frac{1}{\left(2^{n} n !\right)^{1 / 2}} H_{n}(z) \exp \left\{-\frac{z^{2}}{2}\right\} \exp \left\{-\frac{i}{\hbar} E_{n} t\right\} $ und $z = \sqrt{\frac{m \omega}{\hbar}} x$

  • Weitere Fakten

    • Die Energie ist quantisiert mit $E_n = \hbar \omega (n + \tfrac{1}{2})$

    • Die Grundzustandsenergie ist größer als Null: $E_0 = \tfrac{\hbar \omega }{2}$

    • Der Wellenfunktionen des harmonischen Oszillators erfüllen die Unschärferelation; der Grundzustand tut dies mit minimaler Unschärfe

Harmonischer Oszillator als Näherung des Potentials nahe des Minimums. Harmonische Oszillator Wellenfunktionen.

Aus der Vorlesung

Streuung, Bindung und Tunnelung

Der Tunneleffekt beschreibt das Propagieren eines Quants durch eine endlich Potentialbarriere.

Siehe auch das Potentialbarrieren Quiz

Tunneleffekt Idee.

  • Die WKB-Näherung erlaubt es die Tunnelwahrscheinlichkeit $T$ für allgemeine Potentiale zu approximieren
    Sie nimmt an, dass die Amplitude der Wellenfunktion innerhalb der Barriere langsam oszilliert

    $T \simeq \exp \left\{-\frac{2}{\hbar} \int_{x_{1}}^{x_{2}}|p(x)| \mathrm{d} x\right\}\,$ und $\,p(x)=\pm \sqrt{2 m(E-V(x))}$

    $x_{1/2}$ sind die Punkte an denen die Potenitalbarriere berührt wird mit $E = V(x_{1/2})$. (Im obigen Bild ist $x_1 = -a$ und $x_2 = a$)

Beispiel: Der $\alpha$-Zerfall durch die Starke Wechselswirkung nach Gamow

Tunneleffekt: alpha Zerfall Potential.
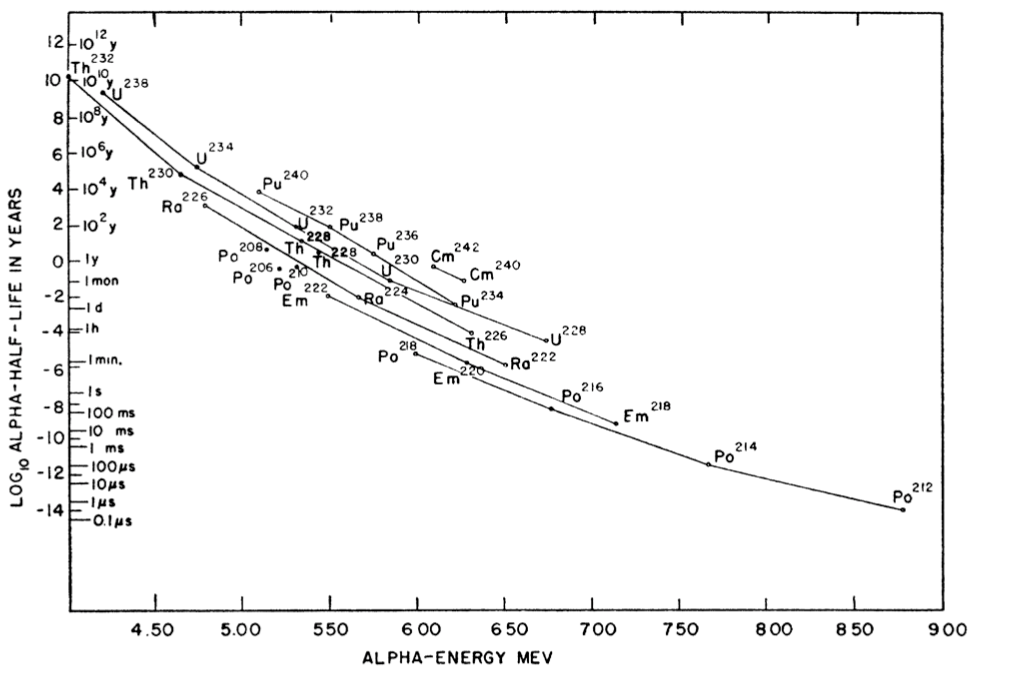
Tunneleffekt: alpha Zerfall Befund.

Potentialannahme + WKB-Approximation bestätigt den experimentelle Skalierung der Halbwertszeit

$$\ln(\tau) = a / \sqrt{E} + b$$

Hausaufgabe Blatt 6

Allgemeine Lösungen der stationären Schrödingergleichung

Im Allgmeinen genügt es eine Basis an Eigenfunktionen des Hamiltonoperators zu finden, sodass alle weiteren Lösungen als Linearkombination dieser Basis dargestellt werden können.

  • Es genügt reelle Lösungen zu betrachten.

  • Für ein symmetrisches Potential ($V(\vec{r})=V(-\vec{r})$) genügt es symmetrische und anti-symmetrische Lösungen zu betrachten.

WKB Quantisierungsbedingungen

Die WKB Approximation gibt Näherungen für die Energieniveaus gebundener Zustände, durch die Quantisierungsbedingung

$$ \int_{x_1}^{x_2} p(x)\mathrm{d}x =\int_{x_1}^{x_2} \sqrt{2m(E-V(x))}\mathrm{d}x =\left(n+\alpha\right) \pi \hbar\,. $$

  • Integrationsbereich für $V(x)< E$, also Integrationsgrenzen aus $E=V(x)$

  • Zahl $\alpha$ anhängig von der Anzahl $W$ an unendlich hohen Potentialwänden:

    $ W=0\Rightarrow \alpha=1/2\,, \quad W=1\Rightarrow \alpha=3/4\,, \quad W=2\Rightarrow \alpha=1\,. $