Leistungsteiler

In der Hochfrequenztechnik sind Leistungsteiler passive Bauelemente, die eine speziell geometrische Anordnung aufweisen. Dabei verteilt die Anordnung die Signalleistung möglichst gleichmäßig auf zwei oder mehrere Tore. Leistungsteiler gibt es in verschiedenen Ausführungen, die sich bezüglich Leistung, Frequenz und Wellengang voneinander unterscheiden. Der Unterschied lässt sich am besten mit Streuparametern beschreiben. Im Folgenden werden verschiedene Leistungsteiler vorgestellt und diskutiert.

1. Wilkinson Leistungsteiler

Der so genannte „Wilkinson Leistungsteiler“ wurde als Schaltungskonzept der Hochfrequenztechnik von Ernest J. Wilkinson im Jahr 1960 veröffentlicht.

Charakteristisch für einen Wilkinson Leistungsteiler ist sein geringer Leistungsverlust, da es schaltungstechnisch angepasst und ausgangsseitig entkoppelt ist. Die Anpassung ist mit einem doppelten Wellenwiderstand zwischen beiden Ausgangstoren gegeben. Die Entkopplung beider Ausgangstore erfolgt, aufgrund der geometrischen $$ \lambda/2 $$ Leitungslänge, zwischen den beiden Ausgangstoren. Dabei verursacht $$ \lambda/2 $$ der Leitungslänge eine Phasendrehung um 180°, die zu einer Aufhebung durch Überlagerung und einer Entkopplung führt.

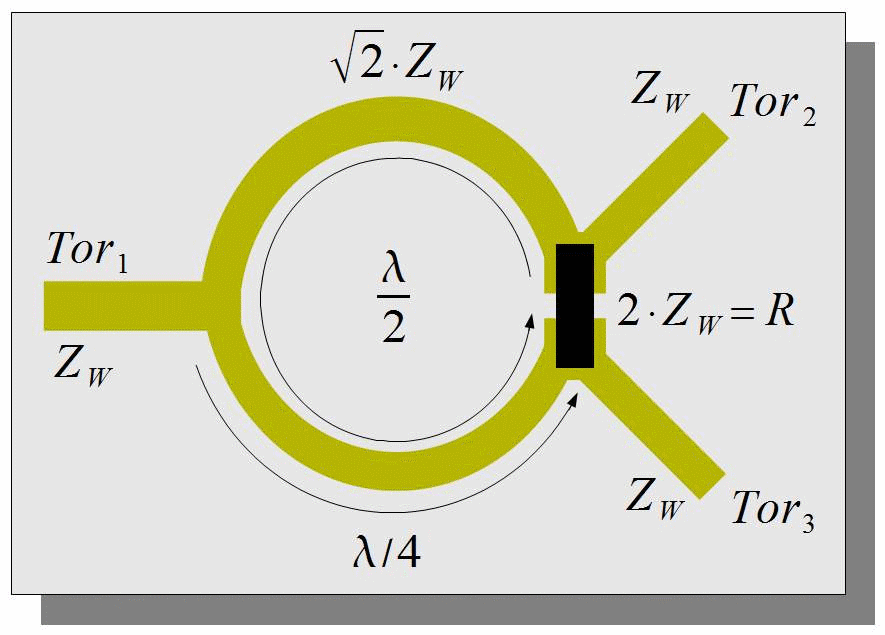
Abbildung 1.0: 3-Tor Wilkinson-Leistungsteiler in Mikrostreifentechnik

$$ \lambda $$ := Wellenlänge, $$ Z_W $$ := Wellenimpedanz der Leitung, $$ R $$ := Abschlussimpedanz.

Am meisten profitiert die Mikrostreifentechnik vom Wilkinson Leistungsteiler. Als passives Schaltungselement wird er durch Leitungsstrukturen mit einem konzentrierten Bauelement, einem Widerstand als Abschluss, realisiert (Abbildung 1.0). Dabei ist die Möglichkeit einer Kaskadierung oft nützlich. Der Vorteil der Kaskadierung ist die geometrisch starre Anordnung, die eine synchron phasengleiche Wellenausbreitung ermöglicht. Oft werden viele parallele Signalpfade auf einem HF-Frontend benötigt. Eine Beispielanwendung hierfür ist das Multikanal-Frontend für ein Antennen-Array-System, wo vielfach das gleiche Signal erforderlich ist, um Zwischenfrequenzen herunter zu mischen oder Trägersignale für mehrere Pfade zu erzeugen.

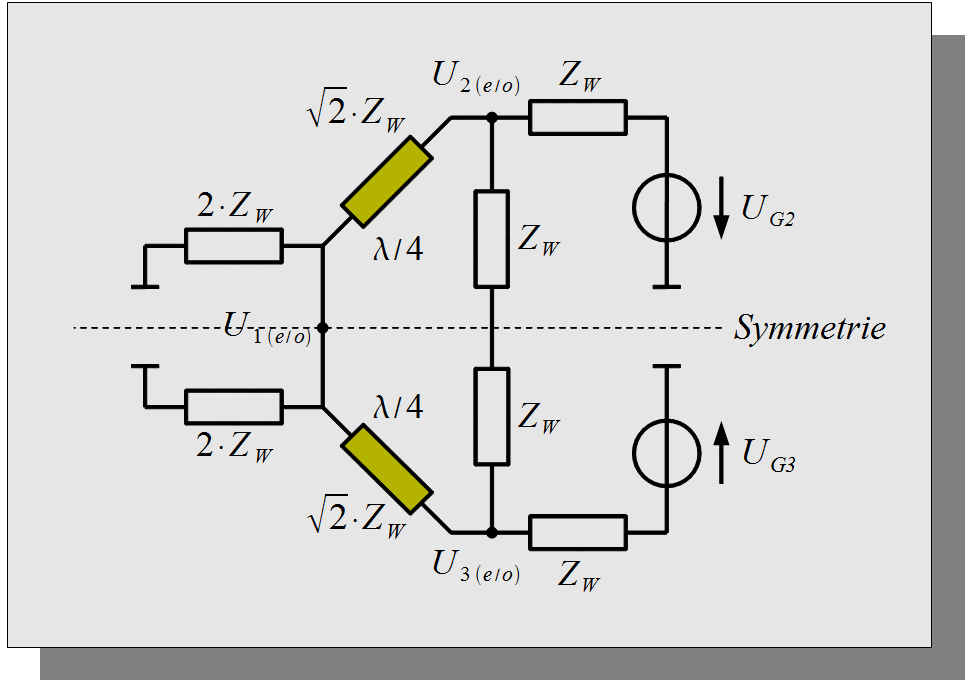
Abbildung 1.1: Ersatzschaltbild für ein 3-Tor Wilkinson-Leistungsteiler

Das Ersatzschaltbild in Abbildung 1.1 dient als Basis zur Berechnung der Wilkinson-Leistungsteiler Eigenschaften, die im Folgenden durch technische Schlussfolgerungen und Berechnung der Streuparameter ermittelt werden. Dazu weist das Ersatzschaltbild zwei Generatorquellen am Tor 2 und 3 auf und ein Massepotential am Tor 1. Die Symmetrieebene in der Abbildung ist durch den symmetrischen Aufbau der Schaltung gegeben. 

1.1 Schlussfolgerungen und Ermittlung der Streuparameter

Die Funktion des Leistungsteilers lässt sich gut durch eine Streuparameter-Matrix darstellen. Die Beschreibung beschränkt sich auf einstufigen Wilkinson Leistungsteiler. Ein mehrstufiger Wilkinsonteiler kann für breitbandige Leistungsteiler verwendet werden.   

Die allseitige Leistungsanpassung mit dem entsprechenden Wellenwiderstand $$ Z_W $$ ergibt eine Reflexionsfreiheit an allen Toren. Für die Streuparameter bedeutet es, dass die Terme in der Diagonale gleich Null sind $$ S_{11} = S_{22} = S_{33} = 0 $$. Des Weiteren führt die Verbindung zwischen Tor 2 und 3 das Signal über eine $$ \lambda/2 $$ Weglänge, die eine Phasenverschiebung von 180° für eine Welle darstellt. Da die Tore 2 und 3 auch über einen Abschlusswiderstand gekoppelt sind, heben sich die Wellenanteile durch Überlagerung auf, sodass keine gegenseitige Kopplung zu Stande kommen kann. Dabei wird auch keine Leistung umgesetzt. Dieser Zusammenhang ergibt für die Streuparameter, dass die Anteile $$ S_{23} = S_{32} = 0 $$ sein müssen. 

Bei einer Einspeisung am Tor 1 teilt sich die Signalleistung, aufgrund der geometrisch symmetrischen Anordnung und gleicher Belastung durch den Abschlusswiderstand an Tor 2 und 3, in zwei gleiche Teile auf. Da die Amplitude quadratisch mit der Leistung zusammenhängt, ergibt sich für die Streuparameter der Faktor $$ \frac{ 1 }{ \sqrt{ 2 } } $$. Zugleich hat eine Leitung einen Einfluss auf die Phasendrehung der Welle. Für die Phase wirkt eine abgeschlossene $$ \lambda/4 $$ Leitung als -90° Phasenverschiebung. Der Zusammenhang kann wie folgt dargestellt werden:

$$ U_2 = U_1 \cdot e^{( \alpha - j \beta \frac{ \lambda }{ 4 } )} = U_1 \cdot e^{( 0 - j \frac{ \pi }{ 2 }) } = U_1 \cdot ( cos ( \frac{ \pi }{ 2 } ) - j sin ( \frac{ \pi }{ 2 } ) ) = -j U_1 $$

mit $$ \alpha = 0 $$ und $$ \beta = \frac{ 2 \pi }{ \lambda } $$.

Diese Zusammenhänge ergeben für die Transmission der Streuparameteranteile $$ S_{21} = S_{31} = \frac{ -j }{ \sqrt{2} } $$. 

In der Praxis kann zum Einen die geometrische Symmetrie nicht ideal in Mikrostreifentechnik realisiert werden und zum Anderen ist $$ \alpha \neq 0 $$. Daher ist diese Betrachtung als eine gute Näherung zu sehen. 

Aufgrund der Symmetrie des Schaltungskonzeptes, lassen sich die restlichen Streuparameter $$ S_{12} $$ und $$ S_{13} $$ durch Gleichtaktanregung (engl. even mode) und Gegentaktanregung (engl. odd mode) ermitteln. Des Weiteren ist die Betrachtung einer Symmetriehälfte für die folgende Herleitung ausreichend. 

1.2 Analyse mit Gleichtaktanregung

Bei einer Gleichtaktanregung, dargestellt in Abbildung 1.2, stellt die Symmetrieachse einen Leerlauf für alle Querelemente dar. In Folge dessen sind die Querelemente an einem Ende offen bzw. im Leerlauf. Deshalb haben diese Elemente schaltungstechnisch keinen Einfluss auf die weitere Berechnung. Für die Analyse wird eine Generatorquelle am Tor 2 angeschlossen und das Tor 1 auf Masse-Potential gelegt. 

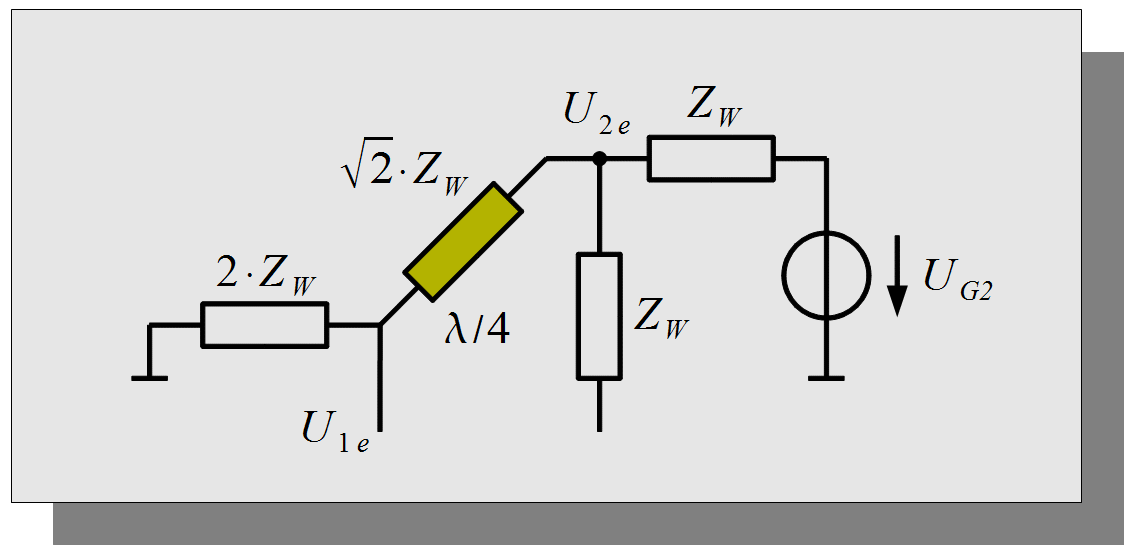
Abbildung 1.2: Ersatzschaltbild bei Gleichtaktanregung

Aufgrund der Aufteilung im Symmetriefall, ergibt sich ein Reflexionsfaktor am Tor 1 zu: 
$$ r_{e} = \frac{ Z - Z_L }{ Z + Z_L } = \frac{ 2 Z_W - \sqrt{2} Z_W }{ 2 Z_W + \sqrt{2} Z_W } = \frac{ 2 - \sqrt{2} }{ 2 + \sqrt{2} } $$ | (1.0),

wobei $$ Z $$ := Abschlussimpedanz, $$ Z_L $$ := Leitungsimpedanz bzw. Wellenwiderstand der Leitung, $$ r_e $$ := Reflexionsfaktor am Tor 1 (even mode).

Die Spannung am Tor 2 ergibt sich mit (1.0) zu:
$$ U_{2e} = U_x ( l = \frac{ \lambda }{ 4 }) = U_x ( e^{ j \frac{ \pi }{ 2 } } + r_e \cdot e^{ -j \frac{ \pi }{ 2 } } ) = j U_x (1 - r_e) $$ | (1.1)

$$ \Rightarrow U_x = \frac{ U_{2e} }{ j(1 - r_e) } = -j \frac{ U_{2e} }{ (1 - r_e) } $$ | (1.2)

Die Spannung am Tor 1 ergibt sich zu:
$$ U_{1e} = U_x ( l = 0 ) = U_x ( e^{ 0 } + r_e \cdot e^{ 0 } ) = U_x (1 + r_e) $$ | (1.3)

$$ \Rightarrow U_x = \frac{ U_{1e} }{ (1 + r_e) } $$ | (1.4)

Zudem ist die Amplitude der am Tor 2 auch: $$ U_{2e} = \frac{U_{G2}}{2} $$ | (1.5)

Mit Gleichungen (1.2), (1.3) und (1.5) ergibt sich zu:
$$ U_{1e} = -j \frac{U_{G2}}{2} \frac{ (1 + r_e) }{ (1 - r_e) } = -j \frac{U_{G2}}{2} \frac{ (1 + \frac{2 - \sqrt{2}}{2 + \sqrt{2}}) }{ (1 - \frac{2 - \sqrt{2}}{2 + \sqrt{2}}) } = -j \frac{U_{G2}}{2} \frac{ (2 + \sqrt{2})(2 + \sqrt{2} + 2 - \sqrt{2}) } {(2 + \sqrt{2})(2 + \sqrt{2} - 2 + \sqrt{2}) } = -j \frac{U_{G2}}{\sqrt{2}} $$ | (1.6)

Mit Gleichungen (1.1), (1.4) und (1.6) ergibt sich zu:
$$ U_{2e} = j U_{1e} \frac{ (1 - r_e) }{ (1 + r_e) } = j(-j) \frac{U_{G2}}{2} \frac{ (1 - r_e) }{ (1 + r_e) } = \frac{U_{G2}}{2} \frac{ (2 + \sqrt{2})(2 + \sqrt{2} - 2 + \sqrt{2}) } {(2 + \sqrt{2})(2 + \sqrt{2} + 2 - \sqrt{2}) } = \frac{U_{G2}}{2} $$ | (1.7)

Des Weiteren kann der richtige Wellenwiderstand für den Halbkreisbogen (Abbildung 1.0) ermittelt werden. Da hier eine Leitungslänge von $$ \lambda/4  $$ vorliegt, kann die einfache $$ \lambda/4- $$ Transformation benutzt werden. 

$$ Z_{L}^2 = Z_{A} \cdot Z_{E} = 2 Z_{W} \cdot Z_{W} = 2 Z_{W}^2 \Rightarrow Z_{L} = \sqrt{2} \cdot Z_{W} $$ 

1.3 Analyse mit Gegentaktanregung

Bei der Gegentaktanregung liegen alle Querelemente auf dem Massepotential (siehe in Abbildung 1.3). Des Weiteren liegt der Wellenwiderstand in der Abbildung in gelb dargestellt ausgangsseitig auch auf einem Massepotential. 

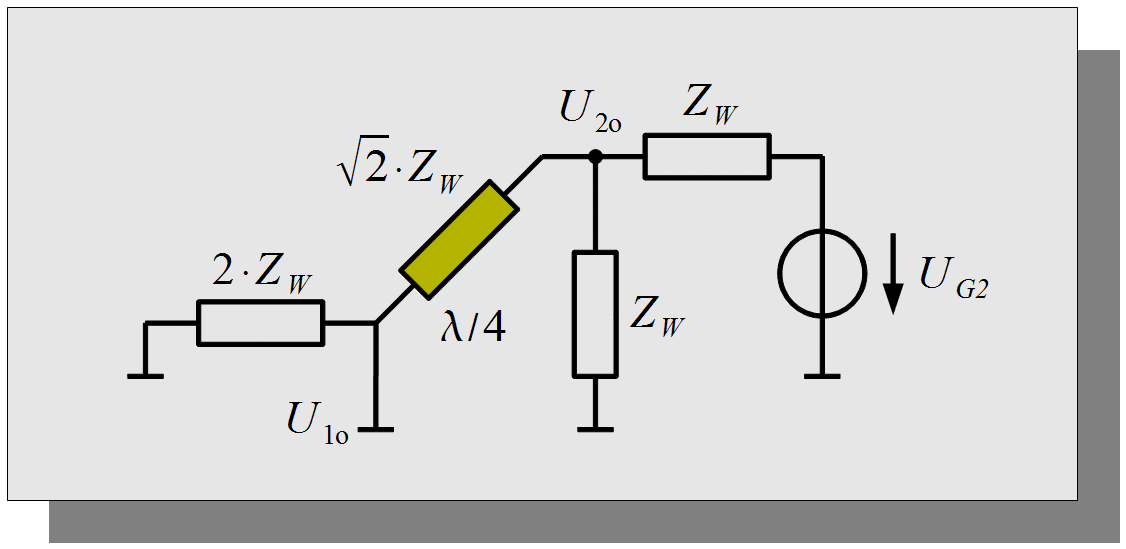
Abb.1.3: Ersatzschaltbild bei Gegentaktanregung

Der Reflexionsfaktor ergibt sich zu: 
$$ r_o = \frac{ Z - Z_L }{ Z + Z_L } = \frac{ 0 - \sqrt{2} Z_W }{ 0 + \sqrt{2} Z_W } = -1 $$ | (1.8), wobei $$ r_o $$ := Reflexionsfaktor am Tor 1 (odd mode).

Die Amplitude am Tor 2 bleibt wie oben gleich: $$ U_{2o} = \frac{ U_{G2 } }{ 2 } $$ | (1.9)

Die Spannung am Tor 1 ergibt sich zu: 
$$ U_{1o} = U_x (l = 0) = U_x (e^0 + r_o \cdot e^0) = U_x (e^0 + (-1) \cdot e^0) = 0 $$ | (2.0)

Damit ergeben sich die restlichen Streuparameter mit (1.6), (1.7), (1.9) und (2.0) zu:
$$ S_{12} = S_{13} = \frac{ U_{1e} + U_{1o} }{ U_{2e} + U_{2o} } = \frac{ -j \frac{U{G2}}{\sqrt{2}} + 0 }{ \frac{U_{G2}}{2} + \frac{U_{G2}}{2} } = \frac{-j}{\sqrt{2}} $$

Weiterhin lässt sich bemerken, dass eine mit Kurzschluss abgeschlossene $$ \lambda/4- $$ Leitung einen Leerlauf am anderen Ende darstellt. Das hat zur Folge, dass die Hälfte des konzentrierten Widerstandes, der in einer Symmetriehälfte dem Wellenwiderstand entsprechen muss. 

$$ \Rightarrow R = 2 \cdot Z_{W} $$ 

1.4 Ergebnis der komplexen Streuparameter-Matrix

$$ \displaystyle \begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix} = \frac{-j}{\sqrt{2}} \begin{bmatrix} 0 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} $$

1.5 Zusammenfassung

Das Wilkinson-Schaltungskonzept ist ein nahe verlustloses und passives Schaltungselement. Es wird gern für eine symmetrische Leistungsteilung eingesetzt. Aufgrund der Symmetrie sind die Ausgangssignale phasengleich. Geometrisch muss die Anordnung für eine bestimmte Betriebsfrequenz ausgelegt werden. Ein breitbandiger Wilkinsonteiler ist ebenfalls möglich. Auf eine breitbandige Erweiterung wurde in diesem Beitrag allerdings nicht weiter eingegangen.  

Weitere Hinweise finden Sie in den unten angegebenen Quellen 1 und 2.

2. Der Rat-Race-Koppler

Abb. 2.1: Rat-Race-Koppler

Der Rat-Race-Koppler findet häufigen Einsatz für die Verkopplung oder Trennung von hochfrequenten Signalen. Dieser Ringkoppler wird auch als 180°-Hybrid bezeichnet. Der Koppler als Mikrostreifenstruktur besteht aus verscheiden Leitungslängen, abhängig von der genutzten Wellenlänge. Die Leitungen zwischen den Toren 1,2,3 und 4 sind jeweils λ/4 lang und die Leitungslänge zwischen Tor 1 und 4 misst 3/4 λ.
Um eine möglichst gute Anpassung zu erreich müssen die Zuleitungen zum Koppler den gleichen Wellenwiderstand von Z_w haben und die Verbindungsleitungen den Wellenwiderstand von $$ Z_W \cdot \sqrt{2} $$.

Durch die gewählten leitungslängen von λ/4 –Leitungstransformatoren und einer λ/2 - Verzögerungsleitung ergeben sich verschiedene Phasenänderungen zwischen den Toren (s. Tabelle 2.1). Der Rat-Race-Koppler weißt im Vergleich eine größere Bandbreite als der Branchline-Koppler auf.

Divider

Als Leistungsteiler wird der Rat-Race-Koppler an einem Tor mit einem Eingangssignal gespeist und an zwei Ausgangstoren erhält man die gleich aufgeteilte Leistung. Ein Tor ist komplett entkoppelt.

Abb. 2.2: Rat-Race-Koppler als Divider

Das Verhalten des „dividers“ ist durch die Überlagerungen der Signale mit unterschiedlichen Phasenverschiebungen zu erklären. Bei der Überlagerung zweier Wellen mit gleicher Amplitude aber einem Phasenversatz von 180° zueinander, kommt es zu einer destruktiven Überlagerung und somit zur Auslöschung der Signale. Findet eine Überlagerung zweier Wellen mit gleicher Phase zueinander statt, so kommt es zu einer konstruktiven Überlagerung und die Signale werden aufaddiert. In der nachfolgenden Tabelle sind für den Fall der Leistungsteilung die zueinander verschiedenen Phasen an den Toren gegeben.

Tabelle 2.1: Verhältnis der Phasen zwischen den Toren

Es ergibt sich somit die folgende Streumatrix für den Rat-Race-Leistungsteiler

$$ \displaystyle S = \frac{-j}{\sqrt{2}} \begin{bmatrix} 0 & 1 & 0 & -1 \\ 1 & 0 & 1 & 0 \\ 0 &1 & 0 & 1 & \\ -1 & 0 & 1 & 0 & \end{bmatrix} $$

Combiner

Nach demselben Prinzip kann der Rat-Race-Koppler als Leitungskombinierer verwendet werden. Werden nun zwei Eingänge mit der Leistung P/2 gespeist, so erhält man an einem Ausgangsport die Addition der Signale und ein entkoppeltes Tor.

Abb. 2.3: Rat-Race-Koppler als Combiner

Gegentaktanregung

Eine weiter besondere Anwendung des Rat-Race-Kopplers ist im Gegentakt Betrieb zu sehen. Durch die Anregung an zwei Ports mit einer Phasenverschiebung von 180° , ergibt sich eine Summation und eine Differenzenbildung der Signale.

Als weiteres Beispiel ist unter dem nachfolgenden Link ein Video der Wellenausbreitung in einem Rat-Race- Koppler zu sehen. Das Video zeigt die Ergebnisse eines Feldsimulationstools. Es ist die eingespeiste Leistung an einem Tor zu erkennen und die sich ausbreitenden Wellen. Ab zwei Ausgangstoren sieht man eine geringere Amplitude als das Eingangssignal. Wie bereits vorgestellt bleit ein Tor entkoppelt.

http://zomobo.net/play.php?id=Po6AgPr2aRY(20.06.12; 08:27)
Animation Video Rat-Race-Leistungsteiler.

3. Der Hybridkoppler (Branchline coupler)

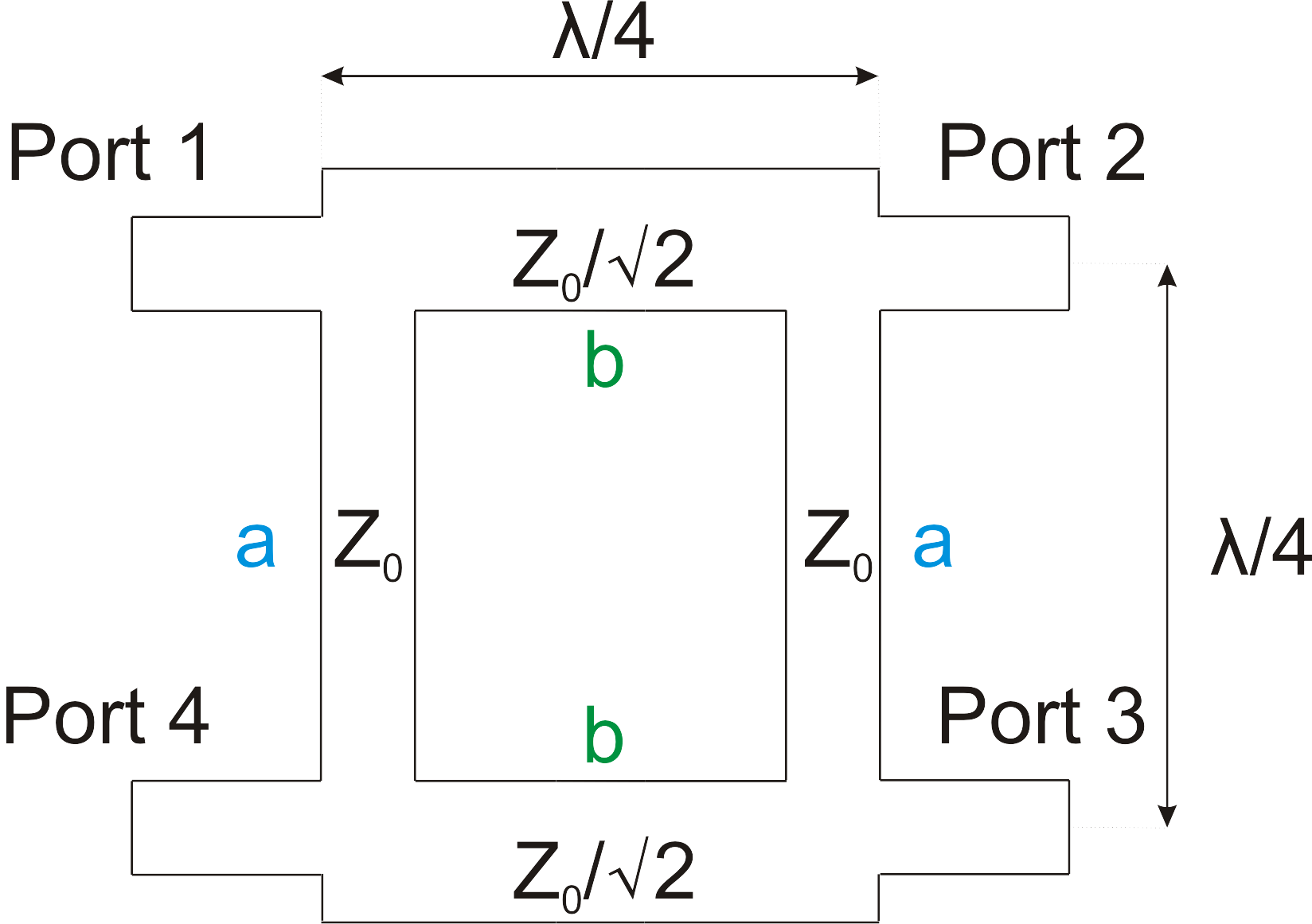
Bei dem Hybridkoppler handelt es sich um einen schmalbandigen Leistungsteiler bzw. Leistungskombinierer. Der symmetrische Aufbau besteht, wie in Abbildung 1 zu sehen ist, aus 4 Ein-/Ausgängen und 4 λ/4-Transformatoren. Die Schmalbandigkeit resultiert aus der verwendeten Geometrie, die auf λ/4-Transformatoren aufbaut und somit auf eine feste Wellenlänge λ ausgelegt ist. Damit der Hybridkoppler breitbandiger wird, können zwei Koppler kaskadiert werden.

Divider

Der Hybridkoppler kann als Leistungsteiler realisiert werden. Hierfür wird am Port 1 ein Signal eingespeist und die Leistung teilt sich zu gleichen Teilen (je -3dB, daher 3-dB-Hybrid) an Port 2 und 3 mit einer Phasendifferenz von 90° auf. Port 4 ist in diesem Zustand entkoppelt.

Das Leistungsverhältnis zwischen Port 2 und 3 kann aber mithilfe der Dimensionierung des Leitungswellenwiderstands der Leitungen a und b variiert werden, z.B. 10dB-Hybrid. Um einen Hybriden zu dimensionieren können folgende Zusammenhänge ausgenutzt werden:

$$ Z_{0,a} = Z_0 \cdot \sqrt{\frac{\frac{P_{Port1}}{P_{Port2}}}{1+\frac{P_{Port1}}{P_{Port1}}}} $$ (3.0)

$$ Z_{0,b} = Z_0 \cdot \sqrt{\frac{P_{Port1}}{P_{Port2}}} $$ (3.1)

Im Internet lassen sich auch mehrere Seiten finden, auf denen man sich diese Werte berechnen lassen kann, z.B. http://www.microwaves101.com/ .

Combiner

Der Hybridkoppler kann auch als Leistungskombinierer benutzt werden. Hierzu müssen zum Beispiel die an Port 2 und 3 eingekoppelten Signale um 90° phasenverschoben sein. So kann das resultierende Signal an Port 1 abgegriffen werden. Port 4 ist in diesem Zustand entkoppelt.

Streuparameter

Mathematisch werden die Streuparameter eines idealen Hybridkopplers mittels folgender Formel beschrieben:

$$ S= \frac{1}{\sqrt{2}}
\begin{bmatrix}
0 & -j & -1 & 0\\
-j & 0 & 0 & -1\\
-1 & 0 & 0 & -j\\
0 & -1 & -j & 0\\
\end{bmatrix}$$


Anwendungen

In der Praxis werden Hybridkoppler zur Aufteilung eines Signals in mehrere Signalpfade benutzt. Diese einzelnen Signale werden danach einzeln bearbeitet, z.B. verstärkt im Sendefall oder im Empfangsfall gemessen.

4. Leitungskoppler

Eine einfache und doch vielfältige Realisierung eines Leistungsteilers findet sich im doppeltsymmetrischen Leitungskoppler (Abb. 4.1). Dieses Viertor besteht aus zwei einander angenäherten Leitungen mit der elektrischen Länge βl, zwischen denen eine kapazitive Kopplung entsteht. Der Grad dieser Kopplung lässt sich über den Abstand der Leitungen einstellen. 

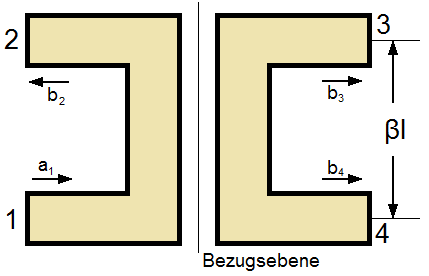
Abbildung 4.1: Leitungskoppler

Unter der Annahme eines homogenen TEM-Systems mit idealen, verlustlosen Leitern ist die Phasenkonstante β der Eigenwellen beider Leiter gleich. Daher lässt sich die Beschreibung über Gleich- und Gegentaktanregung fortführen.

Gleich- und Gegentaktanregung

Eine Gleichtaktanregung (+) wird durch das gleichzeitige Anlegen eines amplituden- und phasengleichen Signals an den Toren 1 und 4 erreicht. Die einlaufende Welle $$ a_1 $$ im Koppelbereich lässt sich also wie folgt aufteilen:

$$ a_1^+ = \frac{1}{2} a_1 , a_4^+ = \frac{1}{2} a_1 $$

Die Gegentaktanregung (-) wird erzielt, indem die Signale um 180° phasenverschoben eingefügt werden, sodass sich das Signal im Koppelbereich zu null aufhebt.

$$ a_1^- = \frac{1}{2} a_1 , a_4^- = - \frac{1}{2} a_1 $$

Die Bedingung hierbei ist, dass sich bei linearer Superposition eine Anregung nur an Tor 1 einstellt:

$$ a_1 = a_1^+ + a_1^- $$

und sich die Einkopplung an den anderen Toren identisch zu null ergibt:

$$ a_2 = a_3 = a_4 = 0 . $$

Hiermit ist es bereits möglich, die Streumatrix des Leitungskopplers zu berechnen.

Direkt ersichtlich sind die durch $$ a_1^+ $$ und $$ a_1^- $$ erzeugten Wellen an Tor 1 und 2:

$$ b_1 = b_1^+ + b_1^- = S_{11}^+ \cdot a_1^+ + S_{11}^- \cdot a_1^- = \frac{1}{2} \cdot ( S_{11}^+ + S_{11}^- ) \cdot a_1 $$

$$ b_2 = b_2^+ + b_2^- = S_{21}^+ \cdot a_1^+ + S_{11}^- \cdot a_1^- = \frac{1}{2} \cdot ( S_{21}^+ + S_{21}^- ) \cdot a_1 $$

Aufgrund der Symmetrie lässt sich dieser Zusammenhang auch durch $$ a_4^+ $$ und $$ a_4^- $$ für die Tore 3 und 4 herstellen:

$$ b_3 = b_3^+ + b_3^- = S_{21}^+ \cdot a_4^+ + S_{11}^- \cdot a_4^- = \frac{1}{2} \cdot ( S_{21}^+ - S_{21}^- ) \cdot a_1 $$

$$ b_4 = b_4^+ + b_4^- = S_{11}^+ \cdot a_4^+ + S_{11}^- \cdot a_4^- = \frac{1}{2} \cdot ( S_{11}^+ - S_{11}^- ) \cdot a_1 $$

Durch Abgleich mit der Streumatrix $$ [b] = [S] \cdot [a] $$ erhält man die Streuparameter:

$$ S_{11} = \frac{1}{2} \cdot ( S_{11}^+ + S_{11}^- ) , $$

$$ S_{21} = \frac{1}{2} \cdot ( S_{21}^+ + S_{21}^- ) , $$

$$ S_{31} = \frac{1}{2} \cdot ( S_{21}^+ - S_{21}^- ) , $$

$$ S_{41} = \frac{1}{2} \cdot ( S_{11}^+ - S_{11}^- ) . $$

Mithilfe von Reziprozität und Symmetrie sind nun auch alle weiteren Streuparameter bekannt:

$$ S_{11} = S_{22} =S_{33} = S_{44} , $$

$$ S_{21} = S_{12} = S_{34} = S_{43} , $$

$$ S_{31} = S_{13} = S_{42} = S_{24} , $$

$$ S_{41} = S_{14} = S_{32} = S_{23} . $$

Kettenmatrix

Durch Einführung der Wellenwiderstände $$ Z_e $$ und $$ Z_d $$ für Gleich- bzw. Gegentaktanregung können die Streuparameter mithilfe der Kettenmatrizen für verlustlose Leitungen beschrieben werden:

$$ \begin{bmatrix} A^+ & B^+ \\ C^+ & D^+ \end{bmatrix} = \begin{bmatrix} cos \beta l & j \frac{Z_e}{Z_0} sin \beta l \\ j \frac{Z_0}{Z_e} sin \beta l & cos \beta l \end{bmatrix} $$

$$ \begin{bmatrix} A^- & B^- \\ C^- & D^- \end{bmatrix} = \begin{bmatrix} cos \beta l & j \frac{Z_d}{Z_0} sin \beta l \\ j \frac{Z_0}{Z_d} sin \beta l & cos \beta l \end{bmatrix} $$

Durch die Korrenspondenz zwischen Ketten- und Streumatrix lassen sich nun die einzelnen Streuparameter berechnen:

$$ S_{11} = \frac{A+B-C-D}{A+B+C+D}, $$

$$ S_{12} = \frac{2 \cdot (AD-BC)}{A+B+C+D}, $$

$$ S_{21} = \frac{2}{A+B+C+D}, $$

$$ S_{22} = \frac{-A+B-C+D}{A+B+C+D}, $$

Beispielhaft wird das Ergebnis für $$ S_{11}^+ $$ angegeben werden:

$$ S_{11}^+ = \frac{ j ( \frac{Z_e}{Z_0} - \frac{Z_0}{Z_e} ) sin \beta l }{ 2 cos \beta l + j ( \frac{Z_e}{Z_0} - \frac{Z_0}{Z_e} ) sin \beta l } $$

Ergebnis

Es zeigt sich, dass die Eingangsreflexion $$ S_{11} $$ sowie die Transmission zu Tor 3 $$ S_{31} $$ identisch null werden, wenn man $$ \frac{Z_e \cdot Z_d}{Z_0^2} = 1 $$ wählt.

Weiter lässt sich zwischen $$ S_{21} $$ und $$ S_{41} $$ eine frequenzunabhängige Phasenverschiebung von 90° erkennen, welche auf die Unitarität für verlustlose und passive Vierpole bei doppelter Symmetrie zurückzuführen ist.

Anwendung 

Eine Anwendung des Leitungskopplers ist die Bestimmung von Messobjekten (MO) anhand ihrer Streuparameter. Schließt man ein MO an Tor 2 an und speist ein Signal über Tor 1 ein, so lassen sich die einfallende Welle an Tor 4, die reflektierte Welle an Tor 3 messen. Dieses Prinzip wird gerne in Netzwerk- oder Spektrumanalysatoren angewandt.

Desweiteren kann der Leitungskoppler als Teil eines Mischers verwendet werden, indem ein RF Signal an Tor 1 und eine Pumpfrequenz an Tor 3 eingespeist und gemeinsam an Tor 4 abgegriffen werden können.

Literaturhinweise

1. Halbleiterschaltungstechnk| Buch in 13. Auflage | U. Tietze
2. Hochfrequenztechnik | Script 2009 | T. Zwick
3. Höchstfrequenztechnik: Grundlagen, Schaltungstechnik, Messtechnik, Planare Antenne; G. Gronau; Springer DE, 2001
4. Hochfrequenztechnik: Hochfrequenzfilter, Leitungen, Antennen; O.Zinke, H. Brunswig; Springer DE, 2000
5. Hochfrequenztechnik: Bauelemente, Schaltungen, Anwendungen; Edgar Voges; Hüttig 2004
6. Internetquellen: http://www.microwaves101.com/ (06.08.2012)
7. Grundlagen der Hochfrequenz-Messtechnik, B. Schiek, Springer 1999