Mischer

Der Mischer

Ein Mischer stellt im Idealfall einen Multiplizierer dar. In der Regel besitzt der Mischer zwei Eingänge für die zu mischenden Signale und einen Ausgang für die Mischprodukte.
Insbesondere in der Hochfrequenztechnik findet er überall dort Anwendung, wo Signale auf eine höhere oder tiefere Frequenz umgesetzt werden müssen.
Abbildung 1 zeigt den Mischer, schematisch dargestellt durch einen Kreis mit einem Kreuz in der Mitte. Die zwei zu mischenden Signale sind das umzusetzende Signal $$ s_{HF} $$ und das Lokaloszillatorsignal $$ s_{LO} $$. Am Ausgang des Mischers sprechen wir vom Zwischenfrequenzsignal $$ s_{ZF} $$. In der Praxis entspricht $$ s_{HF} $$ z.B. dem hochfrequenten, von einer Antenne kommenden Signal und $$ s_{LO} $$ beispielsweise einem lokal erzeugten Signal mit fester Frequenz und Amplitude.

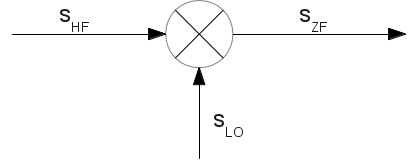
Abb. 1: Idealer Mischer

Führt man zwei periodische Signale einem idealen Mischer zu, so entstehen jeweils zu gleichen Teilen die Summen- wie auch die Differenzfrequenz aus beiden Signalen. Dies lässt sich anhand einer einfachen Rechnung unter Verwendung eines Additionstheorems verdeutlichen:

$$ s_{HF} = a \cdot \cos({\omega}_{HF} \cdot t) $$ (1)
$$ s_{LO} = b \cdot \cos({\omega}_{LO} \cdot t) $$ (2)

$$ s_{ZF} = s_{HF} \cdot s_{LO} = a\cos({\omega}_{HF} \cdot t)b\cos({\omega}_{LO} \cdot t) $$ (3)
$$ s_{ZF} = \frac{1}{2}ab[\cos[({\omega}_{HF}+{\omega}_{LO})\cdot t]+\cos[({\omega}_{HF}-{\omega}_{LO})\cdot t]] $$ (4)

Das ZF-Signal besteht nun aus zwei Anteilen gleicher Amplitude mit verschiedener Frequenz. Der Summenterm mit $$ f_{HF} + f_{LO} $$ bildet das obere Seitenband, der Differenzterm mit $$ f_{HF} - f_{LO} $$ das untere Seitenband. Man spricht hier auch von Aufwärts- und Abwärtsmischen.

Aufwärtsmischung

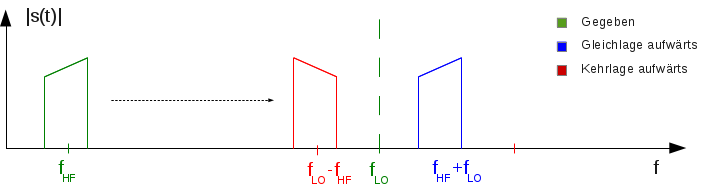
Abb. 2: Aufwärtsmischung

Bei der Aufwärtsmischung liegt die gewünschte Ausgangsfrequenz höher als die Eingangsfrequenz. Es entstehen die in Abbildung 2 gezeigten Mischprodukte. In der Regel ist nur eines der beiden sich ergebenden Bänder von Interesse, das andere wird weggefiltert. Um den Unterschied zwischen Gleich- und Kehrlagemischung zu verdeutlichen, wurde statt einer diskreten Frequenz ein breites Frequenzband mit steigender Amplitude umgesetzt.
Durch die Mischung entstehen nun die Summen- und die Differenzfrequenzbänder $$ f_{HF}+f_{LO} $$ und $$ f_{LO}-f_{HF} $$. Wie man sieht, ergibt sich die Amplitudenverteilung des Differenzspektrums spiegelverkehrt zum ursprünglichen Spektrum. Frequenzanteile die vorher am Anfang des Frequenzbandes lagen (tiefe Frequenz), befinden sich nun am Ende (hohe Frequenz). Dies wird als Kehrlage-Mischung bezeichnet.
Das Summenfrequenzand hingegen hat keine derartige Spiegelung erfahren und wurde deshalb in Gleichlage gemischt. Das hochgemischte Signal in Gleichlage kann mit einem geeigneten Hochpass herausgefiltert werden.

Abwärtsmischung

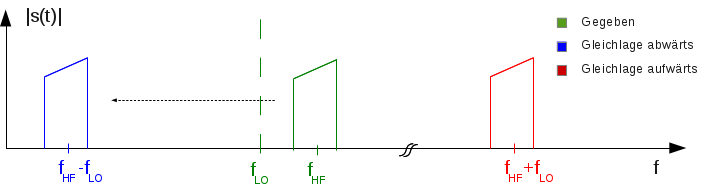
Abb. 3: Abwärtsmischung in Gleichlage

Möchte man eine hohe Eingangsfrequenz auf eine niedrigere Frequenz umsetzen, spricht man von Abwärtsmischung. Liegt die Lokaloszillatorfrequenz unterhalb der Eingangsfrequenz kommt es zu einer Abwärtsmischung in Gleichlage (Abb. 3). Mithilfe eines geeigneten Tiefpasses kann das Signal nun zur Weiterverarbeitung gefiltert werden.

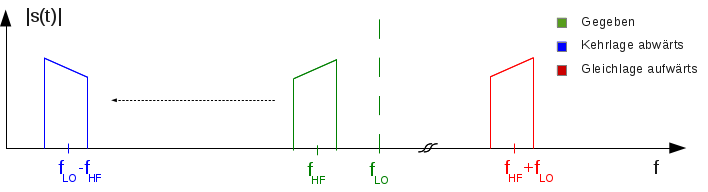
Abb. 4: Abwärtsmischung in Kehrlage

Der Vollständigkeit halber zeigt Abbildung 4 die Abwärtsmischung in Kehrlage. Hier liegt die Lokaloszillatorfrequenz höher als die Eingangsfrequenz wodurch das heruntergemischte Frequenzband wiederrum gespiegelt erscheint.

Mischung am nichtlinearen Bauelement - Parametrische Rechnung

In der Praxis werden Mischer oft nur mithilfe eines einzigen nichtlinearen Bauteils realisiert. In Frage kommen hier z.B. Dioden (insbesondere Schottky-Dioden), Bipolar- oder MOS-Transistoren. Lineare Multiplizierer, welche aus einer größeren Anzahl an Bauelementen bestehen, sind für die Anwendung oft ungeeignet, da sie höhere Rauschzahlen aufweisen.
Um zu verstehen, wie das Mischen an einem nichtlinearen Bauteil, hier an einer Diode, funktioniert, kann der parametrische Ansatz herangezogen werden.
Betrachten wir die Spannungen und Ströme an der Diode. Es seien gegeben die Spannung des Lokaloszillators $$ u_{LO}(t) $$ und die Kleinsignalspannung des HF-Signals $$ \Delta u_{HF}(t) $$. Beide Signale liegen als Summe an der Diode an. Die Amplitude des Lokaloszillators wird nun als sehr viel größer als die des HF-Signals angenommen. In guter Näherung kann eine Taylor-Reihe für den Zusammenhang von Spannung und Strom an der Diode herangezogen werden:

$$ I(u_{LO}(t)+\Delta u_{HF}(t)) = I(u_{LO}(t))+\frac{dI}{dU}\left|_{u_{LO}(t)}\cdot\Delta u_{HF}(t) $$(5)

Der Strom in der Diode besteht also aus einem zeitveränderlichen Strom, der den Arbeitspunkt einstellt, und dem überlagerten HF-Signal $$ \Delta i_{HF}(t) $$. Durch die Annahme, dass es sich bei $$ \Delta u_{HF}(t) $$ um ein Kleinsignal handelt, kann angenommen werden, dass dieses linear mit $$ \Delta i_{HF}(t) $$ verknüpft ist.

$$ \Delta i_{HF}(t) = g(u_{LO}(t))\Delta u_{HF}(t) $$ (6)

Der zeitabhängige Leitwert $$ g(u_{LO}(t)) $$ wird ausschliesslich durch das Lokaloszillatorsignal bestimmt und wird daher auch als Parameter der parametrischen Rechnung bezeichnet.

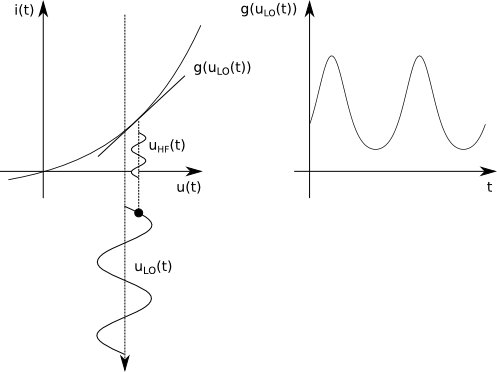
Abb. 5: Steilheit am Bauelement

In Abbildung 5 kann man gut erkennen, wie die Steilheit am Bauelement durch den Lokaloszillator variiert wird. Der Arbeitspunkt, auf den das HF-Signal trifft, wird somit periodisch mit dem LO-Signal verändert. Da das bisher monofrequente LO-Signal nun den Arbeitspunkt auf der exponentiellen Kennlinie der Diode auslenkt, entstehen hierdurch Oberwellen der LO-Frequenz.
Nimmt man für das Lokaloszillatorsignal nun an, dass dieses die Grundkreisfrequenz $$ {\omega}_{LO} $$ besitzt, so kann man dieses mithilfe einer Fourierreihe ausdrücken:

$$ g(u_{LO}(t)) = \sum_{{n}={-\left(\infty\right)}}^{\infty}G_n e^{jn{\omega}_{LO}t$$ (7)

Nun sei das HF-Signal monofrequent und somit gegeben durch:

$$ \Delta u_{HF}(t) = U_{HF}\cos({\omega}_{HF}t) = \frac{1}{2}(U_{HF}e^{j{\omega}_{HF}t}+U^*_{HF}e^{-j{\omega}_{HF}t}) $$ (8)

$$ U_{HF} $$ und $$ U^*_{HF} $$ stellen die Amplitude bzw. die komplex konjugierte Amplitude des HF-Signals dar. Führt man die Multiplikation aus Gleichung 6 durch ergibt sich folgender Term:

$$ \Delta i_{HF}(t) = g(u_{LO}(t))\Delta u_{HF}(t) = \frac{1}{2}\sum_{{n}={-\left(\infty\right)}}^{\infty}(U_{HF}G_ne^{j({\omega}_{HF}+n{\omega}_{LO})t}+U^*_{HF}G_ne^{-j({\omega}_{HF}-n{\omega}_{LO})t})$$ (9)

Lässt man nun nur die HF-Frequenz sowie die heruntergemischte Zwischenfrequenz (ZF) bei $$ {\omega}_{ZF} = {\omega}_{HF}-{\omega}_{LO} $$ zu, was sich in der Praxis aufgrund der gewünschten Filterung ergibt, vereinfacht sich der Term zu:

$$ \Delta i_{HF}(t) = \frac{1}{2}(U_{HF}G_0e^{j({\omega}_{HF})t}+U^*_{HF}G_0e^{-j({\omega}_{HF})t}+
U_{HF}G_{-1}e^{j({\omega}_{HF}-{\omega}_{LO})t}+U^*_{HF}G_{1}e^{-j({\omega}_{HF}-{\omega}_{LO})t}) $$ (10)

Mit der Randbedingung dass $$ G_{-n} = G^*_n $$ kommt man auf:

$$ \Delta i_{HF}(t) = \frac{1}{2}(U_{HF}G_0e^{j({\omega}_{HF})t}+U^*_{HF}G_0e^{-j({\omega}_{HF})t}+
U_{ZF}G^*_{1}e^{j({\omega}_{HF}-{\omega}_{LO})t}+U^*_{ZF}G_{1}e^{-j({\omega}_{HF}-{\omega}_{LO})t}) $$ (11)

Und somit kann man zum Schluss die Matrixschreibweise herleiten:

$$ \left( \begin{array}{ccc} I_{HF}\\I_{ZF}\\ \end{array} \right) = \left( \begin{array}{ccc} G_0 & G_1\\G^*_1 & G_0\\ \end{array} \right)\cdot \left( \begin{array}{ccc} U_{HF}\\U_{ZF}\\ \end{array} \right)  $$ (12)

Hierdurch ergibt sich ein linearer Zusammenhang zwischen dem Ein- und Ausgang des Mischers.

Literatur

[1] B. Schiek: Grundlagen der Hochfrequenzmesstechnik, Springer, 1999

[2] U. Tietze, Ch. Schenk: Halbleiterschaltungstechnik, Springer, 2010

[3] J. Detlefsen, U. Siart: Grundlagen der Hochfrequenztechnik, Oldenbourg, 2009